Zanim wyjaśnię zasadę działania tablicy mieszającej, pozwolę sobie zrobić małą dygresję na temat algorytmów, w których potrzebne informacje przechowuje się w tablicach. Punktem wyjścia jest w nich obserwacja, że uzyskanie dostępu do elementu tablicy jest operacją niemal natychmiastową (chyba że tablica jest tak duża, że nie mieści się w pamięci fizycznej -- ale to zupełnie inna bajka). Dlatego jeżeli mamy do czynienia z funkcją, wywoływaną z argumentami należącymi do stosunkowo niewielkiego zbioru, możemy wszystkie jej wartości obliczyć na początku programu i zapisać w specjalnej tablicy. Następnie, zamiast mozolnie wyznaczać jej wartości w trakcie wykonywania programu, po prostu odczytujemy je z tej tabeli. W ten sposób poświęcamy część pamięci operacyjnej, ale w zamian otrzymujemy szybszy kod. Jednym z najbardziej znanych przykładów takiego kompromisu jest implementacja standardowej funkcji (makroinstrukcji) isdigit, która sprawdza, czy przekazany jej znak reprezentuje cyfrę dziesiętną. Naiwna implementacja tej funkcji może wyglądać następująco:
inline bool IsDigitSlow (char c)
{
return c >= '0' && c <= '9';
}
|
Zauważmy jednak, że funkcję isdigit (char c) można wywołać z co najwyżej 256 różnymi argumentami. Dlatego jej implementację można oprzeć na przedstawionym przed chwilą pomyśle: tworzymy tablicę 256 zmiennych typu bool, przechowujących wartości tej funkcji dla jej wszystkich możliwych argumentów. Ideę tę wcielamy w życie w poniższej implementacji klasy CharTable
class CharTable
{
public:
CharTable ();
bool IsDigit (unsigned char c) { return _tab [c]; }
private:
bool _tab [UCHAR_MAX + 1]; // def. stałej UCHAR_MAX znajduje się w pliku <climits>
};
CharTable::CharTable ()
{
for (int i = 0; i <= UCHAR_MAX; ++i)
{
// tu posługujemy się nieefektywnym algorytmem
if (i >= '0' && i <= '9')
_tab [i] = true;
else
_tab [i] = false;
}
}
CharTable TheCharTable;
|
Przy pomocy obiektu tej klasy możemy bardzo szybko sprawdzić, czy dany znak reprezentuje cyfrę, czy nie. W tym celu wystarczy posłużyć się wyrażeniem
TheCharTable.IsDigit (c) |
W rzeczywistości makroinstrukcję isdigit implementuje się w ten sposób, że aby wyznaczyć jej wartość, sprawdza się wartość pojedynczego bitu odpowiedniego elementu tablicy, inicjowanej statycznie przed rozpoczęciem programu. Każdy bit tej tablicy odpowiada innej właściwości znaku, np. czy reprezentuje on on cyfrę, literę, literę lub cyfrę, biały znak, itp.
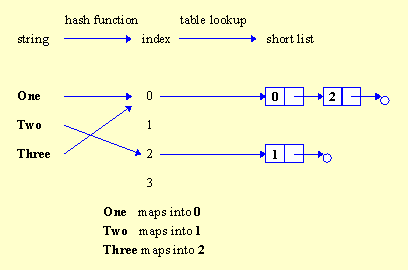
Tablica mieszająca (ang. hash table) jest strukturą danych, w której czas wyznaczania wzajemnego odwzorowania obiektów dwóch dowolnych typów skraca się poprzez zapisanie odpowiednich informacji w specjalnej tablicy. W naszym przypadku tablicą mieszającą posłużymy się w celu stworzenia efektywnej implementacji odwzorowania napisów w zbiór liczb całkowitych. Niestety, nie możemy posługiwać się bezpośrednio napisami jako indeksami do pewnej tablicy zmiennych typu int (innymi słowy, w języku C++ nie można zdefiniować standardowej tablicy liczb całkowitych a, którą indeksowało by się napisami, pisząc np. a["Witaj"] = 8, przyp. tłum.). Możemy jednak zdefiniować pomocniczą funkcję, która dokonywać będzie konwersji napisów na indeksy pewnej tablicy L-elementowej. Zwie się ją funkcją mieszającą lub funkcją skrótu (ang. hash function). Dzięki zastosowaniu tej funkcji proces konwersji napisu w liczbę całkowitą można przeprowadzić w dwóch etapach: najpierw przy pomocy funkcji mieszającej odwzorowujemy napis s w pewną pomocniczą liczbę całkowitą h z przedziału 0,...,L-1, po czym zaglądamy do h-tego elementu specjalnej tablicy, zawierającej poszukiwany wynik odwzorowania napisu s w zbiór liczb całkowitych.
Odwzorowanie mieszające, gwarantujące jednoznaczność pierwszego z opisanych powyżej odwzorowań, nazywane jest doskonałym odwzorowaniem mieszającym (ang. perfect hashing). W praktyce najczęściej trudno jest jednak znaleźć funkcję, realizującą mieszanie doskonałe. Często jest to wręcz niemożliwe -- ilość rożnych napisów jest przecież praktycznie nieskończona, zaś zbiór zmiennych typu int ma zazwyczaj 232 lub 264 elementów, dlatego nie istnieje różnowarościowe odwzorowanie zbioru wszystkich napisów w zbiór liczb typu int (zresztą i tak nie miałoby najmniejszego sensu posługiwać się tablicą, mającą miliardy elementów!!!). Dlatego w praktyce często zmuszeni jesteśmy do posługiwania się niedoskonałą funkcją mieszającą, która od czasu do czasu może odwzorować kilka różnych napisów na tę samą liczbę całkowitą z przedziału 0,...,L-1. W tym przypadku mamy do czynienia z tzw. kolizją. Ponieważ używana przez nas funkcja mieszająca z konieczności może prowadzić do powstawania kolizji, tablica mieszająca nie może odwzorowywać napisu w pojedynczą liczbę całkowitą -- musi raczej przyporządkowywać mu krótką listę liczb całkowitych, tzw. kandydatów, wśród których na pewno znajduje się poszukiwana przez nas liczba. Listę tę musimy następnie przejrzeć element po elemencie w poszukiwaniu interesującego nas napisu s (dlatego jest tak ważne, by lista była krótka, a najlepiej -- jednoelementowa). Po znalezieniu tego napisu od razu wiemy, gdzie się znajduje i jaką ma wartość odpowiadający mu identyfikator id.

Rysunek 13. Funkcja mieszająca przyporządkowuje napisom "One" i "Three" ten sam indeks 0. Aby poradzić sobie z powstałą w ten sposób kolizją, zerowy element tablicy mieszającej zawiera krótką listę, na której zapisano identyfikatory obu napisów (czyli dwie liczby całkowite, 0 i 2).
Aby opisany tu algorytm można było uznać za naprawdę efektywny, ilość przetwarzanych napisów musi być odpowiednio duża. Bezpośrednie sprawdzanie identyczności dwóch napisów wymagałoby, średnio rzecz biorąc, dokonania N/2 porównań. Z drugiej jednak strony, jeżeli rozmiar tablicy mieszającej jest większy od N, odnalezienie danego napisu wymagać będzie, średnio rzecz biorąc, dokonania tylko jednego porównania (oraz wyznaczenia wartości funkcji mieszającej). Rozpatrzmy przykładowo tablicę napisów, przechowującą 100 napisów. Odnalezienie w niej danego napisu poprzez bezpośrednie przeszukiwanie całej tablicy wymagać będzie średnio 50-krotnego porównania napisów. Jeżeli jednak informacje o tych 100 napisach rozłożymy, możliwie jak najbardziej równomiernie, w 127-elementowej tablicy mieszającej, odszukanie danego napisu będzie wymagać dokonania niewiele więcej niż jednego porównania. To oznacza istotne przyspieszenie programu!
Oto definicja klasy HashTable. Jak widzimy, tablica mieszająca jest tak naprawdę tablicą list liczb całkowitych (to są właśnie te "krótkie listy", o których tyle mówiliśmy w tym paragrafie). Większość z nich będzie pusta lub zawierać będzie jeden element. Czasami może dojść do konfliktu (gdy funkcja mieszająca odwzorowuje kilka różnych napisów w ten sam indeks do tablicy mieszającej) -- w tym wypadku niektóre listy będą zawierać więcej elementów.
const int sizeHTable = 127;
// Tablica mieszająca napisów
class HTable
{
public:
// funkcja Find zwraca krótką listę "kandydatów"
List const & Find (char const * str) const;
// umożliwia dodanie kolejnego odwzorowania napisu str w liczbę id
void Add (char const * str, int id);
private:
// funkcja mieszająca
int hash (char const * str) const;
List _aList [sizeHTable]; // tablica (krótkich) list
};
// Funkcja HTable::Find znajduje w tablicy mieszającej listę,
// która może (ale nie musi) zawierać identyfikator napisu str.
List const & HTable::Find (char const * str) const
{
int i = hash (str);
return _aList [i];
}
void HTable::Add (char const * str, int id)
{
int i = hash (str);
_aList [i].Add (id);
}
|
Wybór właściwej funkcji mieszającej jest bardzo ważny -- nie chcemy przecież, by w tablicy mieszającej dochodziło do zbyt wielu konfliktów. Jeden z najlepszych algorytmów polega na arytmetycznym dodawaniu wartości kodu ASCII kolejnego znaku, wchodzącego w skład przetwarzanego napisu, do reprezentacji bitowej bieżącej wartości funkcji mieszającej przesuniętej w lewo o 4 pozycje.
int HTable::hash (char const * str) const
{
// argumentem tej funkcji nie może być napis pusty!
assert (str != 0 && str [0] != 0);
unsigned int h = str [0];
for (int i = 1; str [i] != 0; ++i)
h = (h << 4) + str [i];
return h % sizeHTable; // wyznacz resztę z dzielenia przez sizeHTable
}
|
Jak już wiemy, wartością wyrażenia h << 4 jest wartość zmiennej h przesunięta bitowo w lewo o 4 pozycje (czyli po prostu iloczyn 16*h).
W ostatniej instrukcji funkcji mieszającej wyznaczamy resztę z dzielenia h przez rozmiar tablicy mieszającej. Wartością tą można się następnie od razu posłużyć jako indeksem do tablicy, zawierającej sizeHTable elementów. Rozmiar tablicy również nie został dobrany przypadkowo. Najgorsze są potęgi dwójki -- prowadzą bowiem do powstania wielu konfliktów; okazuje się, że najlepiej posługiwać się liczbami pierwszymi. Zazwyczaj jako rozmiar tablicy mieszającej wystarczy przyjąć liczbę postaci 2n + 1 lub 2n - 1. W naszym przypadku sizeHTable = 127 = 27 - 1, co akurat daje liczbę pierwszą.
Jeżeli funkcję mieszającą wywołamy z argumentem "One", otrzymamy liczbę 114. Wartość tę wyznacza się w następujący sposób:
| znak | kod ASCII (szesnastkowo) | h (szesnastkowo) | h (dziesiętnie) |
|---|---|---|---|
| 'O' | 0x4F | 0x4F | 72 |
| 'n' | 0x6E | 0x55E = 0x4F0 + 0x6E | 1374 |
| 'e' | 0x65 | 0x5645 = 0x55E0 + 0x65 | 22085 |
Ponieważ reszta z dzielenia liczby 22085 przez 127 wynosi 114, identyfikator napisu "One" zostanie zapisany w tablicy mieszającej na liście liczb całkowitych o numerze 114.
Oto prosty test naszej tablicy mieszającej:
int main ()
{
StringTable strTable;
strTable.ForceAdd ("One");
strTable.ForceAdd ("Two");
strTable.ForceAdd ("Three");
int id = strTable.Find ("One");
cout << "One at " << id << endl;
id = strTable.Find ("Two");
cout << "Two at " << id << endl;
id = strTable.Find ("Three");
cout << "Three at " << id << endl;
id = strTable.Find ("Minus one");
cout << "Minus one at " << id << endl;
cout << "String 0 is " << strTable.GetString (0) << endl;
cout << "String 1 is " << strTable.GetString (1) << endl;
cout << "String 2 is " << strTable.GetString (2) << endl;
}
|