Gnuplot krok po kroku
- Uruchom program. (W Linuksie polecam wersję napisaną w Qt, obecnie:
gnuplot5-qt) - Narysuj wykres funkcji
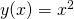
> plot x*x
- W analogiczny sposób narysuj wykres funkcji
 .
. - Narysuj wykres tej samej funkcji, ale w przedziale
![Rendered by QuickLaTeX.com [-10\pi, 10\pi]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-a84a45baec9234789d2d78893b01de3f_l3.png) .
.
> plot [-10*pi:10*pi] sin(x)/x
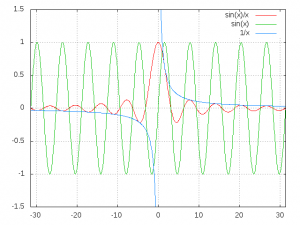
- Aby lepiej zrozumieć, dlaczego on tak wygląda, narysuj na jednym wykresie trzy funkcje:
 ,
, 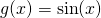 i
i 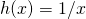
> plot [-10*pi:10*pi] sin(x)/x, sin(x), 1/x
- Prawda, że rysunek jest brzydki? W dodatku niewiele na nim widać. Ogranicz zakres zmienności wartości funkcji do przedziału [-1.5,1.5]
> plot [-10*pi:10*pi][-1.5:1.5] sin(x)/x, sin(x), 1/x
- Powinno być teraz jasne, że wykres funkcji
 dla dużych
dla dużych 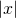 wygląda jak
wygląda jak 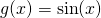 tłumiony funkcją
tłumiony funkcją 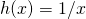 . Żeby coś więcej zobaczyć, narysujmy siatkę (ang. grid)
. Żeby coś więcej zobaczyć, narysujmy siatkę (ang. grid)
> set grid > replot
Komenda
setsłuży do ustawiania domyślnych parametrów wykresu, areplotwykonuje poprzednią komendę plot. - Spróbuj poruszać myszką nad rysunkiem. Gnuplot wyświetla współrzędne punktu wskazywanego przez mysz. Co się dzieje, gdy klikniesz środkowym klawiszem myszy? Co, jeśli poruszasz kółkiem myszy? Do czego w gnuplocie służy prawy klawisz myszy?
- Jak zmienia się sposób wyświetlania wykresów, jeśli poruszasz kółkiem myszy, przytrzymując klawisz shift lub ctrl?
- Do pierwotnego widoku możesz powrócić za pomocą klawisza u. Spróbuj.
- Wróć do okna poleceń gnuplota. Jak działają w nim klawisze ↑ i ↓? Od tej pory nie musisz wpisywać kolejnych poleceń od nowa; wystarczy edytować poprzednie, wybrane tymi klawiszami.
- Wykres jest brzydki. Krzywe są kanciaste.
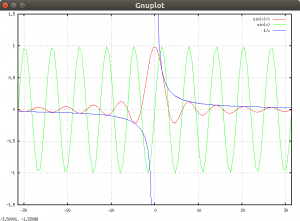 Aby zrozumieć, dlaczego, wyświetl linie oraz symbole (ang. points)
Aby zrozumieć, dlaczego, wyświetl linie oraz symbole (ang. points)
> plot [-10*pi:10*pi][-1.5:1.5] sin(x)/x with linespoints, sin(x) with linespoints, 1/x with linespoints
- Napisanie powyższej instrukcji jest tak pracochłonne, że na pewno nienawidzisz już gnuplota i zastanawiasz się, komu on może w XXI wieku być do czegokolwiek potrzebny? Pierwsza sztuczka: zamiast pełnych nazw poleceń, można pisać skrótami, np.
pzamiastplot,wzamiastwith,lpzamiastlinespoints:p [-10*pi:10*pi][-1.5:1.5] sin(x)/x w lp, sin(x) w lp, 1/x w l
Zapis (dla nowicjuszy) jest mniej czytelny, za to bardziej zwięzły.
- Problem z powyższymi rysunkami jest taki, że gnuplot generuję każdą krzywą ze 100 odcinków. Zwiększmy ich liczbę do 1000:
> set samples 1000 > replot
Komendy te można skrócić do
se sa 1000orazre, ale to chyba przesada: skraca się tylko to, czego używa się często. - Narysuj teraz krzywe bez symboli:
> p [-10*pi:10*pi][-1.5:1.5] sin(x)/x, sin(x), 1/x
Wykres jest teraz dużo bardziej dokładny,
- Jak zapisać wykres w pliku? Trzeba w tym celu wykonać dwie rzeczy: ustawić zmienną output, w której przechowywana jest nazwa pliku, oraz zmienić tzw. terminal, czyli urządzenie rysujące na takie, które zamiast ekranu odpowiadać będzie jakiemuś formatowi graficznemu. Poniższe instrukcje spowodują zapisanie wykresu w pliku o nazwie rys1.png:
> set output "rys1.png" > set terminal png > replot > set terminal pop > unset output
Komenda
set term popprzywraca poprzedni terminal, aunset outputzamyka plik. Warto zapamiętać, że w informatyce „pop” często oznacza „przywróć poprzedni stan”. Słowoterminalmożna skrócić doterm, aoutputdoout.
- Sprawdź, jakie terminale obsługuje twoja wersja gnuplota
> help terminal
- Zapisz wykres w formacie eps (encapsulated PostScript), preferowanym w zastosowaniach, w których wymagana jest wysoka jakość (np. w książkach)
> set terminal postscript eps enhanced color > # oraz pozostałe instrukcje jak w przykładzie powyżej
- Chwila relaksu: sprawdź, jak działa terminal
dumb(jeśli w Twojej instalacji jest obsługiwany). Nie zapomnij wrócić do domyślnego tarminala (set term pop). - Dwa inne popularne formaty obsługiwane przez gnuplot to SVG i JPG. Zapisz wykres w jednym z nich.
- Interaktywne tworzenie „ładnych” wykresów jest żmudne, gdyż wymaga uwzględnienia mnóstwa szczegółów. Praca nad takim wykresem będzie łatwiejsza, jeśli wszystkie komendy zapiszesz w osobnym pliku tekstowym. Utwórz plik „rys1.gp” o następującej treści
set samples 1000 set grid set xlabel "x" set ylabel "f(x)" set mxtics 10 set mytics 5 set key font ",16" set arrow 1 from -5, 1.3 to 0,1 linewidth 1.5 linetype 2 linecolor "black" head set label 1 "sin(0)/0" at -5, 1.4 center font ",15" set term png font "Arial,18" linewidth 1.5 set out "rys.png" p [-10*pi:10*pi][-1.5:1.75] sin(x)/x linewidth 1.5 title "f(x)", sin(x) title "g(x)", 1/x title "h(x)" unset out set term pop
Następnie załaduj go poleceniem
load "rys1.gp"
Sprawdź, jak wygląda rysunek w pliku „rys.png”
- Podmień w tym pliku dwie instrukcje, ustalające terminal i plik docelowy:
set term postscript eps enhanced font "Arial,18" linewidth 2 set out "rys.eps"
pozostawiając resztę bez zmian. Sprawdź, że jakość pliku
epsjest bez porównania lepsza odpng. - Klasyczny PostScript jest czarno-biały jak wydruk ze zwyczajnych drukarek laserowych. Jak rysunkowi z poprzedniego punktu dodać kolor? Wskazówka: musisz coś zrobić z terminalem.
- Teraz lekko zwiększamy zakres użyteczności i poziom trudności zadań. Utwórz plik
dane.txtz następującymi danymi:1 1 1 1 2 2 4 4 3 3 9 8 4 4 16 16 5 5 25 32 6 6 36 64 7 7 49 128 8 8 64 256 9 9 81 516 10 10 100 1024
- Jak widać, plik ma 4 kolumny i 10 wierszy. Narysuj wykres drugiej kolumny względem pierwszej:
plot "dane.txt" with linespoints pointsize 3
- A teraz podobny wykres, ale jako wartości „y” bierzemy dane z kolumny 3:
plot "dane.txt" using 1:3 with linespoints pointsize 3
- Sprawdź, że długie słowa kluczowe można skrócić do 1-2 liter:
p "dane.txt" u 1:3 w lp ps 3
- Skoro jesteśmy na poziomie eksperckim, narysuj czwartą kolumnę w funkcji pierwszej.
- A teraz pierwszą w funkcji czwartej. Niechcący nauczył(a/e)ś się czegoś o funkcjach odwrotnych.
- Teraz poziom ekspercki: wykres pierwiastka z drugiej kolumny względem pierwszej. Zwróć uwagę na symbol dolara, który działa jak selektor kolumny, nawiasy () oraz to, że pierwiastek kwadratowy to sqrt (ang. square root):
p "dane.txt" u 1:(sqrt($2)) w lp ps 2
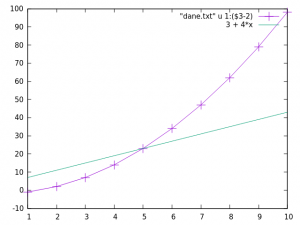
- Oczywiście na jednym obrazku można umieścić wykresy kilku zbiorów danych, funkcji, lub danych i funkcji. Narysuj wykres
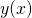 oraz
oraz 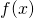 , gdzie
, gdzie 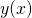 to wykres danych z kolumny 3 pliku „dane.txt” pomniejszonej o 2 w funkcji danych z kolumny 1, a
to wykres danych z kolumny 3 pliku „dane.txt” pomniejszonej o 2 w funkcji danych z kolumny 1, a 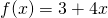 .
.
p "dane.txt" u 1:($3-2) w lp ps 3, 3 + 4*x
- gnuplot może służyć jako prosty kalkulator. Wartości wyrażeń wyświetla się komendą print. Oblicz w ten sposób wartość
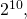
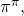
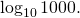
- gnuplot umożliwia definiowanie funkcji. Składnia jest prosta:
nazwa_funkcji(parametr_1,..., parametr_n) = wyrażenie
Zdefiniuj funkcję
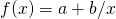
- Poniższa tabela zawiera wynik pomiaru zależności długości fali dźwiękowej (
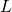 ) od jej częstotliwości (
) od jej częstotliwości (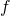 ):
):
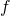
[Hz]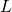
[m]ΔL
[m]500 9.8 0.05 600 8.3 0.05 760 6.4 0.05 985 4.9 0.05 1300 3.8 0.05 1860 2.7 0.05 2980 1.7 0.05 4500 1.1 0.05 6400 0.78 0.005 - Dopasuj parametry funkcji
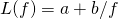 do powyższych danych.
do powyższych danych.
fit f(x) "d.txt" u 1:2:3 via a,b
- Narysuj dane wraz ze słupkami błędów (opcja
using 1:2:3 with error) oraz funkcję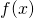
- Czy dopasowanie wygląda „na oko” na wiarygodne? Powiększ w tym celu fragmenty wykresu prawym klawiszem myszy. Pierwotny widok możesz później przywrócić komendą
resetw konsoli gnuplota lub klawiszemuw oknie rysunku. - Kontrolę ilościową jakości dopasowania zapewnia parametr
FIT_STDFIT = sqrt(WSSR/ndf). Czy jego wartość mieści się w przedziale 0.5…2? Jeśli tak, dopasowanie prawdopodobnie jest OK. - Jeśli
FIT_STDFITjest większy od 1, za błąd pomiarowy dopasowywanego parametru przyjmuje się jego „Asymptotic Standard Error” pomnożony przezFIT_STDFIT. Znajdź wartość niepewności pomiarowej i
i 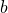 . Wartość asymptotycznego błędu standardowego parametru
. Wartość asymptotycznego błędu standardowego parametru zmiennaprzechowywana jest w zmiennej o nazwiezmienna_err.> print a_err * FIT_STDFIT > print b_err * FIT_STDFIT
- Czy uzyskane przez Ciebie wyniki pozwalają przyjąć tezę, że
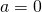 ?
? - Ile wynosi prędkość dźwięku w badanym metalu?
- Dopasuj parametry funkcji
- Jak, bez modyfikacji pliku z danymi, uzyskać wykres danych z poprzedniego zadania, ale w funkcji
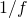 a nie
a nie 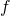 . Taki wykres powinien wyglądać jak linia prosta, a do jego wykonania trzeba użyć opcji
. Taki wykres powinien wyglądać jak linia prosta, a do jego wykonania trzeba użyć opcji using, nawiasów okrągłych i dolara. - Kolejne zadanie do samodzielnego wykonania. Niech
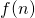 oznacza sumę
oznacza sumę 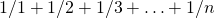 , gdzie
, gdzie 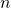 jest liczbą naturalną. Wyznacz
jest liczbą naturalną. Wyznacz 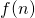 dla
dla 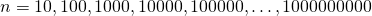 (czyli od dziesięciu do miliarda z mnożnikiem 10). Uczeni w piśmie twierdzą, że dla dostatecznie dużych
(czyli od dziesięciu do miliarda z mnożnikiem 10). Uczeni w piśmie twierdzą, że dla dostatecznie dużych 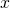 wartość
wartość 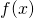 można przybliżyć wzorem
można przybliżyć wzorem 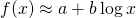 (
(logoznacza tu – i w gnuplocie – logarytm naturalny). Oszacuj wartość stałych i
i 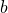 . Wykonaj odpowiedni rysunek z dokładnymi wartościami
. Wykonaj odpowiedni rysunek z dokładnymi wartościami 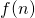 oraz swoją aproksymacją
oraz swoją aproksymacją 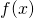 . Nie musisz szacować niepewności
. Nie musisz szacować niepewności  i
i 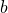 . Uwaga. Do wyznaczenia powyższych sum możesz wykorzystać https://www.wolframalpha.com/input/?i=sum+1%2Fx+from+1+to+1000000000.
. Uwaga. Do wyznaczenia powyższych sum możesz wykorzystać https://www.wolframalpha.com/input/?i=sum+1%2Fx+from+1+to+1000000000. - Po wykonaniu poprzedniego zadania, bez pomocy WolframAlpha oszacuj wartość sumy
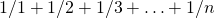 dla
dla 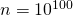 .
. - Prawie na koniec uruchom polecenie
test, które pokazuje możliwości danego terminalu. - (*) A na koniec spróbuj uruchomić program demonstracyjny gnuplota
> load "all.dem"
Problem w tym, że musisz go uruchomić z katalogu, w którym ten plik się znajduje. W tym celu należy zmienić katalog komendą
cd. W linuksie położenie tego pliku można znaleźć poleceniem (w konsoli linuksa a nie gnuplota!)find /usr -name "all.dem"
Pliki z wynikami działania skryptu demonstracyjnego znajdują się na stronie http://gnuplot.info/demos/