Rysunki dwuwymiarowe
Aby narysować wykres funkcji jednej zmiennej lub zbioru danych w formacie (xi, yi), należy przygotować wektor „iksów” i wektor „igreków”, a następnie użyć polecenia plot:
x = -4:0.1:4; # iksy y = (x.^3 + 2*x.^2 + 3*x + 4)./(x.*x+1); # igreki plot(x,y); # bardzo prosty wykres
Powyższy przykład generuje prosty wykres funkcji wymiernej
![]()
Wykres ten jest bardzo prymitywny, spróbujmy więc go nieco urozmaicić.
x = linspace(-4,4,50); y = (x.^3 + 2*x.^2 + 3*x + 4)./(x.*x+1); plot(x, y, "ro-;pewna funkcja wymierna;");
Zmianie uległa definicja wektora x: funkcja linspace (a,b, N) generuje ciąg N równoodległych punktów (ciąg arytmetyczny), z których pierwszy równy jest a, a ostatni – b. Zaletą tego podejścia jest to, że od razu widać, z ilu elementów składa się x. Druga zmiana zaszła w wywołaniu funkcji plot: doszedł trzeci argument, napis "ro-;pewna funkcja wymierna;". Ten trzeci argument definiuje format wykresu i składa się z liter i symboli umieszczonych w napisie w dowolnej kolejności, lecz mających specyficzne znaczenie:
- Styl linii:
-Linia ciągła (opcja domyślna)--Linia przerywana- :
-.Linia przerywana z kropkami
- Styl symbolu reprezentującego punkt danych:
+plusikokółko*gwiazdka.punktxkrzyżykskwadratdromb (ang. diamond)^trójkąt z ostrzem w góręvtrójkąt w dól>trójkąt z ostrzem w prawo<trójkąt z ostrzem w lewoppięciokąthsześciokąt (ang. hexagram)
- Kolor linii i/lub symbolu:
kczarny (ang. blacK)rczerwonygzielonybniebieskimmagentaccyanwbiały
- Opis wykresu (legenda)
;legenda;
Poniższy kod ilustruje, w jaki sposób można narysować wykresy kilku funkcji naraz:
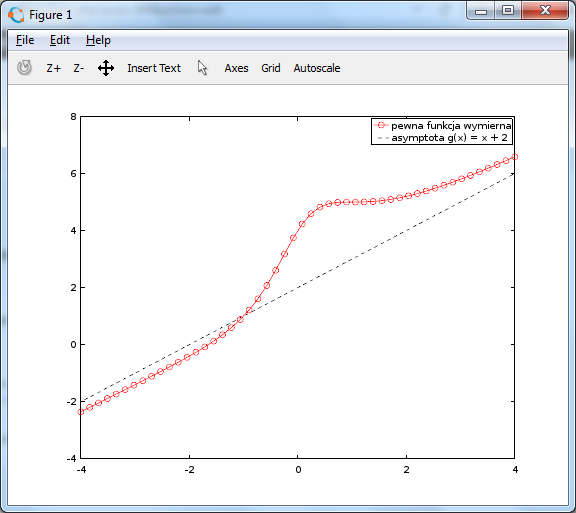
x = linspace(-4,4,50); y = (x.^3 + 2*x.^2 + 3*x + 4)./(x.*x+1); y2 = x + 2; plot(x, y, "ro-;pewna funkcja wymierna;", x, y2, "k--;asymptota g(x) = x + 2;");
Dodajmy jeszcze kilka wodotrysków, jak podpisy osi, tytuł całego rysunku (niestety, bez polskich liter), siatkę, ograniczenie zakresu osi „y” do [-3:8] i zapiszmy wykres na dysku w formacie eps i png:
x = linspace(-4,4,100);
y = (x.^3 + 2*x.^2 + 3*x + 4)./(x.*x+1);
y2 = x + 2;
plot(x, y, "r-;pewna funkcja wymierna;", x, y2, "k--;asymptota g(x) = x + 2;");
xlabel("x");
ylabel("y");
title("Wykres pewnej funkcji wymiernej i jej asymptoty ukosnej");
ylim([-3,8]);
grid on;
print "rys.eps"
print "rys.png"
Dość niezwykłe w powyższym kodzie jest to, że instrukcje modyfikujące wygląd wykresu, np. ylabel, pojawiają się dopiero po komendzie generującej sam wykres (plot). Wiąże się to z tym, że Octave potrafi obsługiwać kilka okienek naraz.
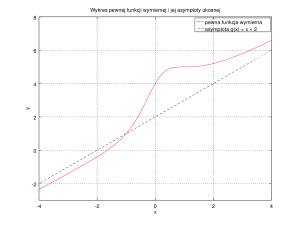
Oto wynik działania powyższego skryptu:
Jak widać, Octave nie posiada bardzo wygodnego interfejsu do tworzenia pięknych wykresów, jednak świetnie nadaje się do szybkiego tworzenia wykresów w miarę czytelnych. Możliwości programu są w tym zakresie naprawdę duże, a funkcje plot i print to tylko niewielka część jej repertuaru.
Alternatywy
Rysunki to nie tylko wykresy, ale także schematy, obrazy rastrowe, mapy konturowe itp. Do szybkiego tworzenia szkiców wykresów dobrze nadają się się m.in.:
- Octave.
- Excel/Libre Office – arkusze kalkulacyjne są użyteczne do analizy danych, umożliwiają szybkie tworzenie wyjątkowo nieestetycznych wykresów.
- Wolfram Alpha – do szybkiego tworzenia prostych wykresów.
- Język Python – do szybkiego tworzenia wykresów i złożonej analizy danych.
Profesjonalne rysunki można wygenerować m.in. następującymi programami:
- Gnuplot– złoty standard naukowców z obszaru STEM w zakresie wykresów naukowych oraz średnio zaawansowanej analizy danych.
- Grace – program dla platformy linuksowej do tworzenia wykresów oraz wstępnej analizy danych; bardziej „okienkowy” od gnuplota, a więc i bardziej „ciążki”, ale chyba mniej elastyczny, na pewno mniej popularny.
- MS Word, Power Point – doskonale nadają się do tworzenia schematów blokowych.
- Inkscape – świetny program do grafiki wektorowej, doskonały do tworzenia bardziej złożonych schematów, diagramów etc.
- Gimp – uniwersalny program do obróbki obrazów rastrowych, niezły odpowiednik komercyjnego Photoshopa. Większość obrazków w tym serwisie pochodzi z Gimpa.
- Paraview – bardzo popularny program do analizy i wizualizacji danych inżynierskich, zwłaszcza rozwiązań równań różniczkowych cząstkowych w 2 i 3 wymiarach.
- C++, Python, FORTRAN lub jakikolwiek inny język programowania – ten wariant umożliwia własnoręczną wizualizację danych w postaci map rastrowych lub grafiki wektorowej. Trzeba tylko nauczyć się (podstaw) jakiegoś standardu kodowania grafiki, np. PostScriptu do grafiki wektorowej lub PPM do grafiki rastrowej.
Quiz
- Jaki rodzaj wykresu wygeneruje format „g:h”?
Zadania
- Narysuj wykres funkcji
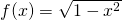 dla -1 ≤ x ≤1.
dla -1 ≤ x ≤1. - Na podstawie poprzedniego punktu narysuj okrąg. Wskazówka: użyj instrukcji pomocniczej
axis ("square"); - Poeksperymentuj z formatem.