Zadanie 1: rozwiązują studenci o nazwiskach zaczynających się od liter A-K
Zadanie 2: rozwiązują studenci o nazwiskach zaczynających się od liter L-Ż
Zadania rozwiązujemy w Octave.
Treść zadań
- Ruch kulki w powietrzu zadany jest układem równań
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} \displaystyle \frac{dx}{dt} &=& v_x\\[3ex] \displaystyle \frac{dy}{dt} &=& v_y\\[3ex] \displaystyle \frac{dv_x}{dt} &=& - b v_x \sqrt{v_x^2 + v_y^2}\\[3ex] \displaystyle \frac{dv_y}{dt} &=& - b v_y \sqrt{v_x^2 + v_y^2} -g \\[3ex] \end{array}\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-f116cc88e718ff7d89e8b3a32a58416f_l3.png)
gdzie
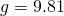 , a
, a 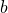 jest pewnym parametrem. W chwili
jest pewnym parametrem. W chwili 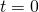 stan kulki opisany jest następującymi parametrami:
stan kulki opisany jest następującymi parametrami:![Rendered by QuickLaTeX.com \[\begin{array}{rcl} \displaystyle x(0) &=& 0\\[3ex] \displaystyle y(0) &=& 0\\[3ex] \displaystyle v_x(0) &=& 20 + N\\[3ex] \displaystyle v_y(0) &=& 20 + N \\[3ex] \end{array}\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-2c2af4c078f01a4647ddabf4283b7465_l3.png)
gdzie
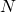 jest resztą z dzielenia numeru indeksu studenta przez 100.
jest resztą z dzielenia numeru indeksu studenta przez 100.- Rozwiąż powyższe równanie dla
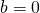 (bardzo ciężka kulka) i
(bardzo ciężka kulka) i 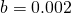 (lekka kulka).
(lekka kulka). - Na jednym wykresie porównaj tory lotu ciężkiej i lekkiej kulki.
- Oszacuj (np. z wykresu), o ile bliżej spadnie lekka kulka, jeżeli podłoże jest płaskie.
- Oszacuj, która kulka spadnie szybciej?
- Rozwiąż powyższe równanie dla
- Rozpatrzmy następujący nieliniowy, nieautonomiczny układ równań różniczkowych zwyczajnych opisujących pewien układ elektroniczny:
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} \displaystyle \frac{dx}{dt} &=& v\\[3ex] \displaystyle \frac{dv}{dt} &=& \mu(1-x^2)v - x+A \sin(\omega t)\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-3fc2f2dc590a5f24cc9f7be088ed1999_l3.png)
- Rozwiąż powyższe równanie dla
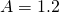 ,
, 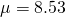 ,
, 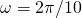 i
i 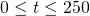 z warunkiem początkowym
z warunkiem początkowym 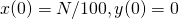 , gdzie
, gdzie 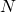 jest resztą z dzielenia numeru indeksu studenta przez 100.
jest resztą z dzielenia numeru indeksu studenta przez 100. - Wykonaj (dwa różne) wykresy
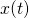 i
i 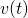 dla
dla 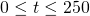 .
. - Czy rozwiązanie ma charakter okresowy (przewidywalny) czy raczej chaotyczny (nieprzewidywalny)?
- Porównaj wrażliwość rozwiązania na drobną zmianę warunków początkowych.
- Rozwiąż powyższe równanie dla
Uwagi:
- Przypomnij sobie treść zadań i samego wykładu o równaniach różniczkowych zwyczajnych. Być może przyda się też plik umieszczony w materiałach z ostatniego wykładu.
- Zidentyfikuj, jakie zmienne są zmiennymi zależnymi (tj. szukanymi funkcjami); ile ich w ogóle jest?
- Napisz funkcję Ovtave realizującą układ równań podany w Twoim zadaniu.
- Sprawdź, że to, co napisał(a/e)ś, na pewno odpowiada treści zadania.
- Zdefiniuj wektor zawierający wartości początkowe.
- Upewnij się, że kolejność zmiennych w wektorze z warunkami początkowymi i w funkcji jest taka sama.
- Zdefiniuj zmienną zawierającą chwile czasu, w których chcesz znać rozwiązanie.
- Rozwiąż układ równań różniczkowych (jedna instrukcja w Octave).
- Wykonaj wykres lub wykresy, zgodnie z treścią zadania.
- Zastanów się, czy rozwiązanie jest rozsądne. W pierwszym zadaniu symulujemy rzut ukośny w ośrodku stawiającym opór, w drugim – układ elektroniczny generujący dźwięk, czasami czysty, czasami szum, ale jego amplituda musi być ograniczona.
- Jeśli rozwiązanie nie jest rozsądne, repeat znajdź błąd, popraw untill succsess.
- Wykonaj ostateczne wykresy (do raportu).
- Napisz krótki raport. W (podpisanym) raporcie umieść co najmniej:
- treść zadania i wartość parametru N
- kod Octave rozwiązujący zadanie (to mogą być 2 pliki, jeżeli funkcję umieścisz w osobnym pliku)
- wykresy
- wyniki liczbowe, jeżeli są wymagane
- kilka zdań komentarza
- Najchętniej widziałbym ten raport na papierze; jeśli nie zdążycie go wydrukować, może być w formie elektronicznej.
Powodzenia!