Zadanie 1: na ocenę bdb

Zadanie 2: rozwiązują studenci, którym wystarczy maksymalnie czwórka z plusem, i których nazwiska zaczynających się od liter A-K

Zadanie 2: rozwiązują studenci, którym wystarczy maksymalnie czwórka z plusem, i których nazwiska zaczynają się od liter L-Ż

Zadania rozwiązujemy w Octave.

Treść zadań

  1. Pewien student miał pecha wyznać, że spory problem przy rekrutacji do firmy na stanowisko testera oprogramowania sprawiła mu słaba znajomość języka angielskiego. Dlatego zadanie na ocenę bdb wymaga umiejętności sięgania do różnych źródeł, w tym tych w języku angielskim. Zajrzyjmy więc do amerykańskiego podręcznika równań różniczkowych zwyczajnych, http://www.mat.univie.ac.at/~gerald/ftp/book-ode/ode.pdf. Na stronie 5 znajdujemy tam układ równań różniczkowych zwyczajnych opisujący ruch ciała niebieskiego wokół nieruchomej masy umieszczonej w początku kartezjańskiego układu współrzędnych (równania 1.11). Rozwiąż te równania, przyjmując następujące wartości parametrów równania oraz warunki początkowe:
    • \gamma M = 0.0002959
    • x(0) = 1.38133346
    • y(0) = 0
    • z(0) = 0
    • v_x(0) = 0
    • v_y(0) = 0.015305031
    • v_z(0) = 0

    Zanim przystąpisz do rozwiązywania powyższych równań, odpowiedz (sobie) na następujące pytania:

    • Dlaczego nie podałem wartości parametru 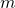 m występującego w oryginalnych równaniach?
    • Co oznacza zapis \ddot{x}?
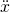    • Jakiego rzędu są to równania i jak sobie z tym poradzić?
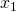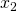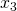    • Jaki jest związek zmiennych x_1, x_2 i x_3 użytych w oryginalnych równaniach z użytymi przez mnie zmiennymi 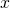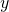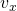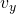x, y, z, v_x, v_y i v_z?

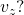
    Rozwiązanie powinno zawierać odpowiedzi na sześć pytań:

    • Jak wygląda wykres 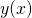y(x) dla pełnego obiegu ciała wokół środka układu?
    • Ile trwa okres 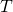T obiegu tego ciała wokół środka układu współrzędnych?
    • Czy wartość zmiennej 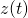z(t) zawsze równa się 0?
    • Jak wygląda wykres prędkości w funkcji czasu 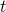t, dla 0 \le t \le T?
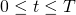    • Ile wynosi stosunek prędkości maksymalnej do minimalnej w tym ruchu?
    • Zakładając, że jednostką odległości jest  jednostka astronomiczna,  jednostką czasu doba ziemska, a masa spoczywająca w środku układu współrzędnych to nasze Słońce, odpowiedz na pytanie, ruch jakiej planety opisują powyższe warunki początkowe?
    • Jeśli  także odpowiesz na pytanie dodatkowe, jakie mogą być główne źródła drobnych odchyleń Twojego rozwiązania od wartości podanych w Wikipedii, to zasłużysz na ocenę 5,5, choć takiej niestety w czasach USOS-a wpisać już nie można.

    Wskazówka: Jest to stosunkowo łatwe zadanie: rozwiązanie go zajęło mi mniej czasu niż wpisanie tu jego treści; a także mniej czasu niż przeliczenie parametrów i warunków początkowych na jednostki astronomiczne, dni ziemskie i masy Słońca. Czyli – do roboty!

  2. Rozpatrzmy następujący układ równań

        \[\begin{array}{rcl} \displaystyle \frac{dx}{dt} &=& 1 + x^2y - b x - x \\[3ex] \displaystyle \frac{dy}{dt} &=& bx - x^2y \\[3ex] \end{array}\]

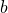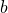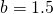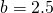    gdzie  b jest pewnym parametrem. Rozwiąż powyższe równanie dla dwóch wartości b: b = 1.5 oraz b= 2.5. Dla każdej z tych wartości 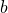b wygeneruj dwa rozwiązania: jedno dla warunku początkowego 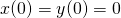x(0)=y(0)=0, a drugie dla 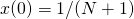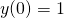x(0) = 1/(N+1), y(0) = 1, gdzie 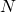N oznacza resztę z dzielenia numeru Twojego indeksu przez 20. Przedstaw rozwiązania za pomocą dwóch wykresów 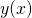y(x), osobno dla każdego 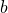b. Na każdym wykresie powinny więc znajdować się dwie krzywe otrzymane dla rożnych warunków początkowych, ale tych samych 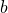b. Spróbuj sformułować ogólne  wnioski odnośnie charakteru rozwiązań powyższych równań dla 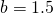b=1.5 i b=2.5.

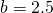  3. Rozpatrzmy następujący układ równań:

        \[\begin{array}{rcl} \displaystyle \frac{dx}{dt} &=& ax - bxy\\[3ex] \displaystyle \frac{dy}{dt} &=& xy - y \\[3ex] \end{array}\]

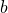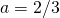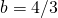    gdzie a, b są pewnymi parametrami. Przyjmij a=2/3 i b=4/3. Rozwiąż to równanie dla czterech stanów początkowych:

    • x(0) = 2, y(0) = 2
    • x(0) = 1, y(0) = 1/2
    • x(0) = 3, y(0) = 1 + 1/(N+1)
    • x(0) = 1, y(0) = 2 + 1/(N+1),

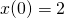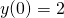
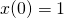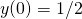
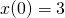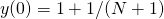
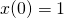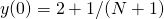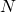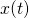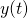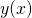    gdzie N oznacza resztę z dzielenia numeru Twojego indeksu przez 20. Wykonaj wykresy x(t), y(t) oraz y(x) (na każdym z nich po 4 krzywe odpowiadające każdemu z powyższych warunków początkowych). Jaki charakter ma rozwiązanie (jest zbieżne do jednego punktu, rozbieżne do nieskończoności, okresowe czy chaotyczne?).

Uwagi:

  • Przypomnij sobie treść zadań i samego wykładu o równaniach różniczkowych zwyczajnych.  Być może przyda się też plik umieszczony w materiałach z ostatniego wykładu.
  • Zidentyfikuj, jakie zmienne są zmiennymi zależnymi (tj. szukanymi funkcjami); ile ich w ogóle jest?
  • Napisz funkcję Ovtave realizującą układ równań podany w Twoim zadaniu.
  • Sprawdź, że to, co napisał(a/e)ś, na pewno odpowiada treści zadania.
  • Zdefiniuj wektor zawierający wartości początkowe.
  • Upewnij się, że kolejność zmiennych w wektorze z warunkami początkowymi i w funkcji jest taka sama.
  • Zdefiniuj zmienną zawierającą chwile czasu, w których chcesz znać rozwiązanie.
  • Rozwiąż układ równań różniczkowych (jedna instrukcja w Octave).
  • Wykonaj wykres lub wykresy, zgodnie z treścią zadania.
  • Zastanów się, czy rozwiązanie jest rozsądne. Na przykład w pierwzym zadaniu rozwiązujemy zagadnienie ruchu planety, więc spodziewamy się ujrzeć raczej niezbyt spłaszczoną elipsę.
  • Jeśli rozwiązanie nie jest rozsądne, repeat znajdź błąd, popraw untill succsess.
  • Wykonaj ostateczne wykresy (do raportu).
  • Napisz krótki raport. W (podpisanym) raporcie umieść co najmniej:
    • treść zadania i wartość parametru N (zadania 2, 3)
    • kod Octave rozwiązujący zadanie (to mogą być 2 pliki, jeżeli funkcję umieścisz w osobnym pliku)
    • wykresy
    • wyniki liczbowe, jeżeli są wymagane
    • kilka zdań komentarza
  • Najchętniej widziałbym ten raport na papierze; jeśli nie zdążycie go wydrukować, może być w formie elektronicznej.

Powodzenia!