Octave rzadko kiedy bywa używany jak zwykły kalkulator do wyznaczania wartości gotowych wyrażeń matematycznych. Jego prawdziwa siła objawia się dopiero wtedy, gdy potraktujemy go jak język programowania, w którym przygotowuje się skrypty, czyli programy napisane w języku Octave. Takie skrypty z reguły zawierają zmienne i funkcje definiowane przez użytkownika.
Spis treści
Definiowanie i rodzaje zmiennych
Definiowanie zmiennych jest banalnie proste: piszemy jej nazwę, znak =, a po nim wartość zmiennej, np.:
>> a = 1 a = 1
Dużo ciekawsza jest kwestia rodzaju zmiennych, jakich możemy używać w Octave. W niniejszym kursie skoncentrujemy się na najbardziej użytecznych typach danych:
- Skalary
- Skalary są to liczby, np.
123,-3.14,1.2e-10. Niezależnie od zapisu, skalary reprezentowane są przez Octave jako tzw. liczby zmiennopozycyjne podwójnej precyzji (IEEE-754 double).
Uwaga: Octave umożliwia też deklarowanie skalarów innych typów, np. całkowitych (8, 16, 32 i 64 bitowych, ze znakiem i bez), zmiennopozycyjnych w pojedynczej precyzji oraz zespolonych. Przykłady skalarów zespolonych:i,1 + 3i,1.2 - 3.4i. Przykłady skalarów całkowitoliczbowych: int8(9), uint64(1). Używanie skalarów innych typów niż domyślny jest jednak w Octave dość nienaturalne, wymaga doświadczenia i nie będzie tutaj omawiane. - Wektory
- Wektory są to ciągi skalarów. Definiujemy je, podając wartości elementów oddzielone przecinkami, np.:
>> a = [1, 2, 3, 4] a = 1 2 3 4
Uwaga: przecinki można pominąć, ale może prowadzić to do subtelnych błędów podczas interpretacji wyrażeń. Dostęp do wartości n-ego elementu wektora
azapewnia wyrażeniea(n):>> a(2)=3 a = 1 3 3 4
Jak widać, pierwszy element wektora n-elementowego to
a(1), a element ostatni toa(n). Oznacza to, że Octave należy do rodziny języków w której obowiązuje tzw. one-based indexing.Wektory można łatwo rozszerzać o nowe elementy:
>> a = [a, 7, [10,100]] a = 1 3 3 4 7 10 100 >> a(10) = 10 a = 1 3 3 4 7 10 100 0 0 10
Liczbę elementów wektora można zbadać funkcją
length>> length(a) ans = 7
W powyższych przykładach mieliśmy do czynienia z tzw. wektorami wierszowymi. Octave rozpoznaje też wektory kolumnowe. Kolejne elementy wektorów kolumnach oddziela się od siebie średnikami:
>> v = [1; 2; 5] v = 1 2 5
- Macierze
- Elementami wektorów kolumnowych mogą być nie tylko liczby, ale i wektory wierszowe. Oto przykład definicji
mjako wektora kolumnowego o dwóch elementach, z których każdy jest dwuelementowym wektorem wierszowym:>> m = [[1, 2]; [3, 4]] m = 1 2 3 4
Takie uogólnione wektory nazywamy macierzami. Macierze są podstawowym typem danych w Octave.
Macierz o
nwierszach imkolumnach zwie się „macierząnnam.” Jeżelim=n, to macierz zwie się kwadratową. W powyższym przykładziemjest więc macierzą kwadratową o dwóch wierszach i dwóch kolumnach, czyli „2 na 2”.Macierze można też interpretować jako wektory wierszowe, których elementy są wektorami kolumnowymi:
m = [[1; 3], [2; 4]] m = 1 2 3 4
Zapis macierzy zwykle upraszcza się jeszcze bardziej, po prostu podając wartości elementów w kolejnych wierszach i kolumnach:
m = [1, 2; 3, 4] m = 1 2 3 4
Liczbę wierszy dowolnej macierzy zwraca funkcja
rows, liczbę kolumn zwraca funkcjacolumns, a funkcjasizezwraca liczbę wierszy i kolumn jako wektor „1 na 2”:>> rows(m) ans = 2 >> columns(m) ans = 2 >> size(m) ans = 2 2
Aby uzyskać dostęp do elementu leżącego w
w-tym wierszu ik-tej kolumnie macierzym, piszemym(w,k):>> m(1,2) ans = 2
Uwaga! Dla Octave skalary i wektory to pewne specjalne rodzaje macierzy: skalary to macierze „1 na 1”, wektory wierszowe to macierze „1 na n”, a wektory kolumnowe to macierze „n na 1”.
- Zakresy
- Zakresy to specjalne typy danych ułatwiające zapis i operacje na wektorach, których elementy tworzą ciąg arytmetyczny. Definicje zakresów zawierają wartość pierwszego elementu ciągu, opcjonalnie – wartość różnicy między jego dwoma kolejnymi wyrazami oraz wartość maksymalną, której elementy ciągu nie mogą przekroczyć. Wartości te oddziela się od siebie dwukropkami, przy czym jeżeli pominie się środkową liczbę, Octave założy, że jej wartość wynosi 1. Dlatego wyrażenie
>> 1:4
definiuje zakres odpowiadający ciągowi
[1, 2, 3, 4]. Analogicznie>> 1 : 0.5 : 4.1
odpowiada wektorowi
[1, 1.5, 2, 2.5, 3, 3.5, 4].Zakresy nie tylko upraszczają zapis, ale przede wszystkim umożliwiają optymalizację działania programu. Np. jeżeli zdefiniujemy zmiennąawyrażeniem>> a = 1:100000
to Octave zarezerwuje dla tej zmiennej zaledwie 24 bajty (3 liczby zmiennopozycyjne). Równoważny tej zmiennej wektor musiałby mieć 100 000 elementów i zajmowałby w pamięci operacyjnej aż 800 000 bajtów.
- Napisy
- Napisy to ciągi liter ujętych w znaki cudzysłowu (lub apostrofy):
>> a = "ala ma kota" a = ala ma kota
Transpozycja macierzy
Transpozycja macierzy to zamiana jej kolumn na wiersze i wierszy na kolumny. W Octave transpozycję macierzy wykonuje się za pomocą specjalnego operatora ' (apostrof). Oto prosty przykład:
>> m = [1, 2, 3; 4, 5, 6] m = 1 2 3 4 5 6 >> b = m' b = 1 4 2 5 3 6
W powyższym przykładzie b jest macierzą transponowaną do m, tj. b czytana kolumnami wygląda tak samo, jak m czytana wierszami.
Jednym z najważniejszym zastosowaniem transpozycji jest zamiana wektorów wierszowych na kolumnowe, wektorów kolumnowych na wierszowe i definiowanie „zakresów kolumnowych”. Tę ostatnią cechę ilustruje następujący przykład :
>> v = [1:4]' v = 1 2 3 4
Uwaga: Jeżeli macierz m ma elementy zespolone, to wyrażenie m' oznacza sprzężenie hermitowskie m. Transpozycję macierzy zespolonej oznacza się operatorem .' (kropka apostrof), np.
m = v.'
Dla macierzy rzeczywistych oba zapisy (z kropką lub bez) są równoważne.
Zapisywanie i odczytywanie zmiennych z pliku
W przypadku bardziej zaawansowanych obliczeń niezwykle ważna jest umiejętność zapisywania i wczytywania danych z plików. Szczególnie istotne jest zapisywanie końcowych wyników żmudnych obliczeń i wyników obliczeń pośrednich, które być może zechcemy kontynuować w przyszłości.
Aby zapisać dowolną zmienną, np. wektor a = [1,2,3,4,100], posługujemy się poleceniem save:
>> save "a.mat" a
Pierwszym argumentem tego polecenia jest zwykle nazwa pliku (tu: a.mat). Następnie podajemy wykaz zmiennych, które chcemy w tym pliku zapisać (tu: jedna zmienna a). Oto przykład instrukcji zapisującej 3 zmienne, a, x i m:
>> save "axm.txt" a x m
Jeżeli nie podamy żadnych zmiennych, Octave zapisze w pliku wszystkie zdefiniowane aktualnie zmienne.
>> save "sesja.txt"
Aby odczytać tak zapisane zmienne, stosujemy polecenie load:
>> load "axm.txt"
Warto zwrócić uwagę na to, że funkcja load nie tylko wczytuje wartości zmiennych, ale też nadaje im zapisane w piku nazwy.
Obie funkcje, save i load, posiadają mnóstwo dodatkowych opcji i potrafią obsługiwać dane w wielu formatach, w tym w formatach binarnych programu Matlab.
Who & whos
Po wczytaniu zmiennych z pliku warto wydać polecenie who
>> who Variables in the current scope: a ans j z
które wyświetla nazwy wszystkich zdefiniowanych aktualnie zmiennych. Jeszcze więcej informacji uzyskamy poleceniem whos:
>> whos Variables in the current scope: Attr Name Size Bytes Class ==== ==== ==== ===== ===== a 1x100000 24 double c ans 1x1 16 double j 1x1 1 uint8 z 1x1 16 struct Total is 100003 elements using 57 bytes
Warto zwrócić uwagę, że w powyższym przykładzie udało się zapisać ponad 100 000 elementów w zaledwie 57 bajtach pamięci.
Clear
Octave często bywa wykorzystywany do obliczeń wymagających ogromnych ilości pamięci. W takich przypadkach nieoceniona bywa możliwość zwolnienia pamięci przez niepotrzebne już obiekty. Służy do tego polecenie clear:
>> clear z
Octave GUI
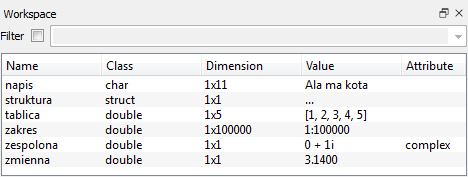
Wykonanie niemal wszystkich powyższych czynności znacznie upraszcza się w okienkowej wersji Octave. Program ten może wyświetlić trzy okienka: File Browser, Workspace i Command History. W szczególności aby załadować dane z pliku zapisanego poleceniem save, wystarczy odszukać go w okienku File Browser i dwukrotnie kliknąć myszką. Z kolei okienko Workspace pozwala na bieżąco śledzić wartości zmiennych (zwłaszcza skalarnych), a okienko Command History ułatwia tworzenie skryptów na podstawie historii poleceń.
Quiz
- Czym różnią się w Octave następujące zmienne:
>> a = 1 >> b = 1.0 >> c = 1e0
- Jak w Octave zapisuje się wektory wierszowe?
- Jak w Octave zapisuje się wektory kolumnowe?
- Czym różnią się następujące zmienne:
>> a = [1 2 3]; >> b = [1, 2, 3]; >> c = [1; 2; 3];
- Jaki jest związek skalarów, wektorów wierszowych i wektorów kolumnowych z macierzami?
- Co to są zakresy? Czym różnią się od wektorów?
- Co to jest transpozycja macierzy? Jak oznacza się ja w Octave?
- W jaki sposób można łatwo zamienić wektor kolumnowy w wierszowy?
- W jaki sposób zapisuje się zmienne Octave w zewnętrznych plikach?
- W jaki sposób wczytuje się zmienne Octave z plików?
- Jak zwolnić pamięć zajmowaną przez zmienną?
- Jak sprawdzić, ile miejsca w pamięci operacyjnej zajmują poszczególne zmienne?
Zadania
- Utwórz wektor
vo elementach1, 2, 5, 10i zapisz go w plikuv.mat. - Po wykonaniu poprzedniego zadania zamknij program, otwórz go ponownie i wczytaj zawartość pliku
v.mat. Sprawdź, że w programie z powrotem pojawiła się zmiennav. - Dla zmiennej
vz poprzedniego punktu sprawdź, jak Octave interpretuje wyrażenia>> v + v >> v + 1 >> v * 2 >> v'
- W pliku „equation.mat” znajduje się definicja kilku zmiennych zapisanych w binarnym formacie programu Matlab.
- Wczytaj ten plik do programu Octave.
- Sprawdź, że w programie pojawiły się nowe zmienne (
who). - Sprawdź, ile wierszy i kolumn ma zmienna
X(size,columns,whos). - Wyznacz najmniejszą, największą i średnią wartość elementów
Xoraz ich medianę (funkcjamimin,max,mean,median). - Narysuj wykres
X(plot (X);) - Zapisz
Xw pliku „x.txt” i sprawdź, że plik ten rzeczywiście ma format tekstowy. - Sprawdź, że plik binarny zajmuje mniej miejsca niż tekstowy.