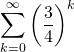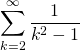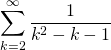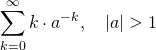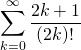Wykład
Quiz
Quiz zawiera pytania, na które odpowiedź powinno się umieć podać z głowy.
- Ciąg arytmetyczny składa się z 200 elementów. Pierwszy z nich ma wartość -10, a wartością ostatniego jest 60. Ile wynosi suma tego ciągu?
- 1 + 2 + 4 + 8 + … + 210 = ???
- Do czego w
Octavesłużą polecenia:cumsumdiffplotsemilogxsemilogyloglog
- Jak w konwencji sumacyjnej Einsteina wygląda zapis:
- iloczynu skalarnego dwóch wektorów, tj.
![Rendered by QuickLaTeX.com \[\sum_{j=1}^{3} a_j b_j\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-2bfffe8be18f1cfde00444e078f51de6_l3.png)
- energii kinetycznej, tj.
![Rendered by QuickLaTeX.com \[\sum_{j=1}^{3} \frac{v_j v_j}{2}\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-eb59788208e82e81f2d140ecc8cfd213_l3.png)
- iloczynu skalarnego dwóch wektorów, tj.
- Uwzględniając odpowiedzi na poprzednie pytanie zinterpretuj znaczenie równania (9) na stronie http://www.cfd-online.com/Wiki/Navier-Stokes_equations.
- Ile wynosi granica ciągu
![Rendered by QuickLaTeX.com \[a_n = \frac{n^3 + 2n^2 +3n + 4}{4 - 3n + 2n^2 - n^3}.\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-c35ce691f2373c67eaa281fc284cf5e3_l3.png)
- Czy granica ciągu o elementach wymiernych może być niewymierna?
- Jak za pomocą pojęcia granicy ciągów oraz zbioru liczb wymiernych skonstruować zbiór liczb rzeczywistych?
- Ile wynosi suma szeregu
![Rendered by QuickLaTeX.com \[1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \ldots\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-e5d1dd85cf94dc16154255d1381270fa_l3.png)
- Czemu równe są granice
![Rendered by QuickLaTeX.com \[\lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-c41489cf0aa961ca632de2227355a448_l3.png)
oraz
![Rendered by QuickLaTeX.com \[\lim_{n\to\infty} \left(1-\frac{1}{n}\right)^n.\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-1538c27faed3bc81a58502397d69ae8d_l3.png)
- Podaj przykład ciągu mającego granicę niewłaściwą.
- W jakim przypadku znajomość granicy dwóch ciągów (an) i (bn) nie wystarcza do stwierdzenia istnienia i ewentualnej wartości granicy ciągu (an/bn)?.
- Spójrz na stronę w angielskiej Wikipedii poświęconą wykresom półlogarytmicznym (ang. semi-log plots).
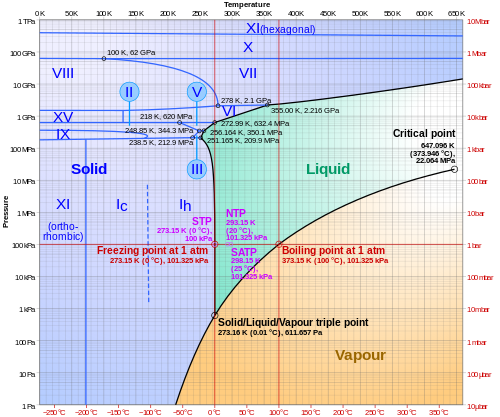
- Dlaczego do sporządzenia zamieszczonego tam wykresu fazowego wody użyto wykresu półlogarytmicznego typu lin-log?
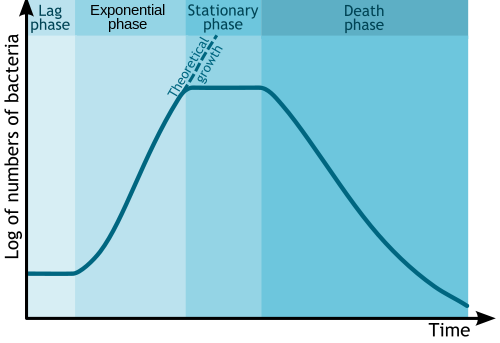
- Dlaczego do schematycznego zilustrowania zależności liczebności kultury bakterii od czasu również posłużono się wykresem półogarytmicznym typu lin-log? Czy istnieje związek pomiędzy nazwą drugiej fazy wzrostu, exponential phase, a kształtem wykresu w odpowiadającym jej obszarze?
- Dlaczego do sporządzenia zamieszczonego tam wykresu fazowego wody użyto wykresu półlogarytmicznego typu lin-log?
Zadania
- Wyznacz sumy skończone:
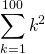
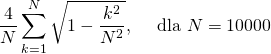
Uwaga. Powyższe wyrażenie z całkiem niezłą dokładnością przybliża pole koła o promieniu 1.
- Znajdź następujące sumy nieskończone:
- Wyznacz granice:
- Na podstawie wartości ostatniej z powyższych granic zaproponuj przybliżony wzór na n!.
- Wyznacz granicę niewłaściwą
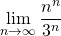
- Na wykładzie omówiłem następujący program:
n = 1:1000; y = abs(sin(1./n)./(1./n) - 1); plot (y, "+;lin-lin;"); xlim([0,20]); pause (2); semilogx(y, "+;log-lin;"); pause(2); semilogy(y, "+;lin-log;"); pause(2); loglog(y, "+;log-log;"); pause(2); loglog(n, y, "+;log-log;", n, 1./n.^2, ";1/n^2;"); pause(2); loglog(n, y, "+;log-log;", n, 1./n.^2/6, "r;1/6n^2;");
- Uruchom ten program.
- Wykresy jakiego ciągu są przezeń wyświetlane?
- Zmodyfikuj go tak, by można było za jego pomocą określić szybkość zbieżności ciągu
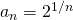 do granicy (równej 1).
do granicy (równej 1).
- Poniższy program (Octave) wyznacza kilka pierwszych elementów ciągu Viete’a, który jest zbieżny do 2/π, i na tej podstawie wyświetla kolejne przybliżenia liczby π:
N = 10; x = zeros(1,N); x(1) = sqrt(2); for i = 1:(N-1) x(i+1) = sqrt(2 + x(i)); wynik = 2 * 2^i/prod (x(1:i)); disp ([i, wynik, pi - wynik]); endfor
- Uruchom ten program.
- Oszacuj prędkość zbieżności tego algorytmu jako algorytmu wyznaczania wartości liczby π.
- Przy jakiej dokładności wyznaczenia liczby π dokładność uzyskiwana w Octave zaczyna odbiegać od wyników, jakich można się spodziewać na podstawie tempa zbieżności ciągu dla kilkunastu pierwszych wyrazów?
- Zapoznaj się z wpisem Espilon maszynowy na Wikipedii.
- (*) Oszacuj prędkość rozbieżności szeregu harmonicznego, 1 + 1/2 + 1/3 + 1/4 + …