Spis treści
Wykład
Wzory fundamentalne
| funkcja | pochodna funkcji | przykład |
|---|---|---|
| wyrażenie | pochodna | przykład |
|---|---|---|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
Quiz
Ten Quiz rozwiązujemy w głowie, na tablicy lub na kartce papieru.
- Oblicz funkcje pochodne następujących funkcji:
- Niech
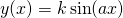 . Oblicz:
. Oblicz:
- O pewnych funkcjach
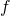 i
i 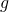 wiadomo, że
wiadomo, że 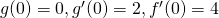 . Ile wynosi pochodna funkcji złożonej
. Ile wynosi pochodna funkcji złożonej 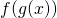 w punkcie
w punkcie 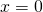 ?
? - Rozpatrzmy funkcję
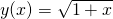 .
.
- Znajdź równanie prostej, która aproksymuje tę funkcję w pobliżu punktu
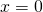 .
. - Uzasadnij, że dla dostatecznie małych
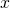 wartość wyrażenia
wartość wyrażenia 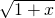 można przybliżyć wyrażeniem
można przybliżyć wyrażeniem 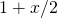 . Uwaga: jest to tak często używane przybliżenie, że warto je zapamiętać.
. Uwaga: jest to tak często używane przybliżenie, że warto je zapamiętać. - Oszacuj w pamięci wartość wyrażeń
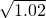 oraz
oraz 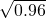 .
.
- Znajdź równanie prostej, która aproksymuje tę funkcję w pobliżu punktu
- Samochód jedzie trasą wokół Los Angeles. Jest to specjalny samochód firmy Google, w którym nie ma kierowcy, za to jest pasażer oraz mnóstwo czujników. Wiadomo, że po 30 minutach samochód przejechał dokładnie 12 km i 113 m i miał wtedy prędkość 7 m/s.
- Oszacuj, jak daleko od punktu startu znajdzie się samochód po 30 minutach i 5 sekundach jeśli wiadomo, że w tym czasie nie hamował ani nie przyspieszał gwałtownie.
- Jaki jest związek pomiędzy tym problemem a poprzednim zadaniem? Wskazówka: prędkość chwilowa to pochodna drogi po czasie.
- Czy możemy w ten sposób wiarygodnie szacować położenie tego samochodu po 1ms, 1s, 1 min, 1 godzinie?
- Jaki jest związek odpowiedzi na poprzednie pytanie z dokładnością aproksymacji funkcji („gładkiej”) funkcją liniową?
- Wg danych GUS, w dniu 30 VI 2014 r. Polskę zamieszkiwało 38 483 957 obywateli. W roku 2014 przyrost naturalny w Polsce wynosił
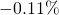 .
.
- Oszacuj liczbę ludności Polski pod koniec 2014 r.
- Jaki jest związek tego problemu z pochodnymi?
- Czy na podstawie przytoczonych powyżej danych można wiarygodnie szacować stan ludności Polski w 2020 r? W 2050 r?
- Czy odpowiedź na pytania z poprzedniego punktu ma związek z dokładnością aproksymacji funkcji („gładkiej”) funkcją liniową, nawet jeśli liczba ludności nie jest funkcją gładką i różniczkowalną (bo ma wartości ze zbioru liczb naturalnych)?
Zadania
W tym tygodniu zadań do rozwiązywania przy komputerze nie ma…