Spis treści
Wykład
Wzory fundamentalne
| funkcja | całka funkcji |
|---|---|
| wzór | komentarz |
|---|---|
| |
liniowość |
| całkowanie przez części | |
| całkowanie przez zamianę zmiennych, |
|
| związek całki oznaczonej z nieoznaczoną | |
| całkowanie jest operacją odwrotną do różniczkowania | |
| różniczkowanie jest operacją odwrotną do całkowania |
Quiz
- Załóżmy, że znasz prędkość
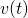 pewnego obiektu w każdej chwili t oraz jego położenie w chwili
pewnego obiektu w każdej chwili t oraz jego położenie w chwili 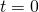 i chcesz wyznaczyć jego położenie w dowolnej chwili t,
i chcesz wyznaczyć jego położenie w dowolnej chwili t, 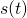 . Czy skorzystasz z całek czy pochodnych?
. Czy skorzystasz z całek czy pochodnych? - Załóżmy, że znasz położenie
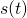 pewnego obiektu w każdej chwili t i chcesz wyznaczyć jego prędkość w dowolnej chwili t,
pewnego obiektu w każdej chwili t i chcesz wyznaczyć jego prędkość w dowolnej chwili t, 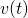 . Użyjesz całek czy pochodnych?
. Użyjesz całek czy pochodnych? - Niech
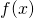 będzie pewną ciągłą i różniczkowalną funkcją. Uprość następujące całki:
będzie pewną ciągłą i różniczkowalną funkcją. Uprość następujące całki:
- Funkcję specjalną (tzw. funkcję błędu)
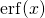 definiuje się jako całkę
definiuje się jako całkę
![Rendered by QuickLaTeX.com \[\displaystyle \mathop{\mathrm{erf}}(x) = \frac{2}{\sqrt\pi}\int_0^x e^{-t^2}\, \mathrm{d}t.\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-37136716289ab1acfd302b585f1c69e3_l3.png)
Oblicz pochodną tej funkcji, czyli
![Rendered by QuickLaTeX.com \[\frac{d}{dx} \mathop{\mathrm{erf}}(x)\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-a190c1bb9b4ea0c4c7a0c5e4227f7041_l3.png)
- W całce
![Rendered by QuickLaTeX.com \[\displaystyle I = \int 3\exp(3x-1)\, dx\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-6917e13c30f0caa859e726cebca20f56_l3.png)
chcemy zastosować podstawienie
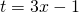 .
.- Wyznacz zależność między
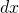 i
i 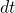 ;
; - Podaj postać całki
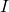 jako całki zmiennej
jako całki zmiennej 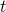 ;
; - Rozwiąż całkę
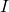 w zmiennej
w zmiennej 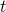 ;
; - Wyraź rozwiązanie jako funkcję oryginalnej zmiennej
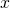 .
.
- Wyznacz zależność między
- Ćwiczenie z terminologii: które z poniższych całek są całkami nieoznaczonymi, które – oznaczonymi, a które są całkami właściwymi, a które – niewłaściwymi:
- Pole koła, objętość kuli. Obejrzyj film umieszczony na stronie https://www.youtube.com/watch?v=whYqhpc6S6g. Jak widać, koło o promieniu
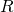 można traktować jak sumę pierścieni o promieniach
można traktować jak sumę pierścieni o promieniach  biegnących od 0 do
biegnących od 0 do 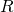 , każdy o polu powierzchni
, każdy o polu powierzchni 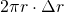 . Prowadzi to do wniosku, że pole koła o promieniu R można wyrazić za pomocy całki
. Prowadzi to do wniosku, że pole koła o promieniu R można wyrazić za pomocy całki
![Rendered by QuickLaTeX.com \[S(R) = \int_0^R 2\pi r\, dr\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-713828dd9222e33004b388c9989d7f5b_l3.png)
.
Analogicznie kulę o promieniu R można rozpatrywać jako sumę sfer o powierzchni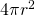 i grubości
i grubości 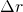 , gdzie
, gdzie 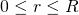 . Wynika stąd, że
. Wynika stąd, że![Rendered by QuickLaTeX.com \[V(R) = \int_0^R 4\pi r^2\, dr\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-4bab20a22245fc06d04e0edeab591a3d_l3.png)
Wyznacz wartości powyższych całek i wyprowadź w ten sposób wzory na pole koła i objętość kuli,
- (*) Oblicz
![Rendered by QuickLaTeX.com \[\displaystyle I = \int x\exp(x)\, dx.\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-4e4b1cb3e730190e4efd81810558e49c_l3.png)
W tym celu:
- Oblicz
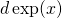
- Wykaż, że
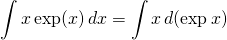
- Stosując metodę całkowania przez części wykaż, że
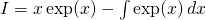
- Wyprowadź stąd wzór na
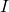 .
.
- Oblicz
Zadania
- Wyznacz całki nieoznaczone z mojego starego podręcznika do analizy matematycznej:
- Wyznacz całki nieoznaczone, których w normalnym kursie analizy matematycznej nie uświadczysz, gdyż rozwiązania nie są funkcjami elementarnymi:
- Oblicz
- Korzystając z Octave, wyznacz wartości całki Fresnela
![Rendered by QuickLaTeX.com \[S(x) = \int_0^x \sin(t^2)\, dt\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-30957cf130bb0e8d89caadc74f2a28ba_l3.png)
dla
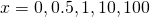 . Porównaj wyniki uzyskane w Octave z wynikami otrzymanymi w WolframAlpha
. Porównaj wyniki uzyskane w Octave z wynikami otrzymanymi w WolframAlpha - Korzystając z Octave, wyznacz wartość całki
![Rendered by QuickLaTeX.com \[\int_0^\infty \frac{\sin(t^2)}{t}\, dt\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-39dc02a226fc0610197ca762cbb912c5_l3.png)
- Wypróbuj kilka metod Octave, np.
quad,quadl,quadv,quadgkiquadcc. - Porównaj wynik z tym, jaki podaje Wolfram Alpha
- Sprawdź, jakie oszacowanie wielkości niepewności wartości całki zwraca ta metoda Octave, która zwraca jakikolwiek wynik.
- Wypróbuj kilka metod Octave, np.
- Aby zrozumieć, dlaczego Octave ma kłopoty z powyższą całką, jeśli granica całkowania dąży do nieskończoności, wykonaj wykres funkcji
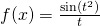 oraz funkcji
oraz funkcji
![Rendered by QuickLaTeX.com \[S_1(x) = \int_0^x \frac{\sin(t^2)}{t}\, dt\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-cc99a050e1c5ffb4438b13732edde192_l3.png)
f = @(x) (sin (x .^ 2) ./ x) x = 1e-8:0.0001:10; # lub: x = linspace(1e-8, 10, 100000); z = cumtrapz(x, f(x)); plot (x, f(x), "b;funkcja;") hold on plot (x, z, "r;calka;") ylim([-0.5,1]); hold off;
Uwaga. Akurat dla tej całki z samego rysunku można oszacować jej wartość graniczną z przyzwoitą dokładnością 3 cyfr znaczących. Powyższy przykład ilustruje, dlaczego całki niewłaściwe są szczególnie trudne. Gdyby górna granica całkowania była nie większa niż ok. 25, bezpośrednie metody numeryczne sprawowałyby się znakomicie. Powyżej tej wartości trzeba dzielić przedział całkowania na mniejsze odcinki, by ograniczyć liczbę oscylacji funkcji. Dla jeszcze większych górnych granic całki trzeba sprytu, np. próbować zmienić postać funkcji podcałkowej poprzez zamianę zmiennych lub całkowanie przez części (tak robi Wolfram Alpha), obliczyć całkę zupełnie inną metodą, np. poprzez całkowanie odpowiedniego szeregu potęgowego lub w inny sposób przekształcić problem do postaci bardziej użytecznej w metodach numerycznych.