ODE (ang. ordinary differential equations) to angielski skrótowiec oznaczający „równania różniczkowe zwyczajne”.
Spis treści
Wykład
Khan Academy
Równania różniczkowe pierwszego rzędu, a zwłaszcza: Wstęp do równań różniczkowych.
Quiz
- Jaki jest rząd następujących równań różniczkowych zwyczajnych:
-
- Które z poniższych równań różniczkowych są liniowe?
-
- Jak wygląda rozwiązanie ogólne równań postaci
![Rendered by QuickLaTeX.com \[\frac{dx}{dt} = f(t)\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-c3e67959fd41c4a3e9073597297714ba_l3.png)
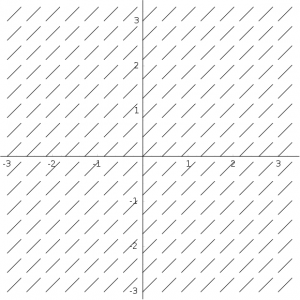
- Przyporządkuj pola kierunków odpowiednim równaniom:
-
- Na podstawie wykresu (z poprzedniego zadania) odpowiadającego równaniu
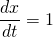 zaproponuj ogólną postać rozwiązania tego równania. Sprawdź, przez bezpośrednie podstawienie swojej propozycji do równania, czy masz rację.
zaproponuj ogólną postać rozwiązania tego równania. Sprawdź, przez bezpośrednie podstawienie swojej propozycji do równania, czy masz rację. - Niech
x = 1:1:100; y = 1:1:100; [xx, yy] = meshgrid(x, y);
- Z ilu elementów składa się obiekt
xx? - Jaka jest wartość wyrażenia
xx(1,1)? - Jaka jest wartość wyrażenia
xx(17, 18)? - Jaka jest wartość wyrażenia
yy(17, 18)? - Jaka jest wartość wyrażenia
xx(1,:)? - Jaka jest wartość wyrażenia
xx(:,1)?
- Z ilu elementów składa się obiekt
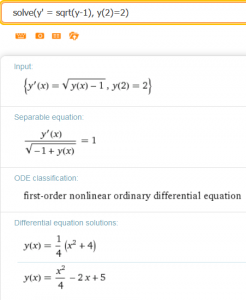
- Poniższy zrzut ze strony WolframAlpha sugeruje, że równanie
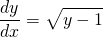 z warunkiem początkowym
z warunkiem początkowym 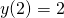 ma dwa rozwiązania:
ma dwa rozwiązania: 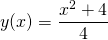 oraz
oraz 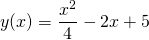 . Sprawdź, czy oba z nich rzeczywiście spełniają powyższe równanie różniczkowe w
. Sprawdź, czy oba z nich rzeczywiście spełniają powyższe równanie różniczkowe w 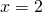 .
.
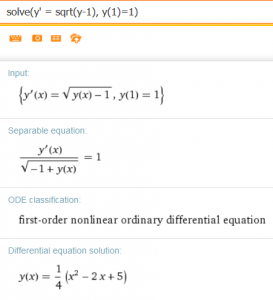
- Poniższy zrzut ze strony WolframAlpha sugeruje, że jedynym rozwiązaniem równania
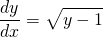 z warunkiem początkowym
z warunkiem początkowym 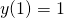 jest
jest 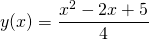 . Sprawdź, że istnieje jeszcze jedno rozwiązanie tego problemu:
. Sprawdź, że istnieje jeszcze jedno rozwiązanie tego problemu: 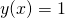 .
.
- Rozpatrzmy prawą stronę równania różniczkowego z poprzedniego zadania,
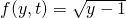 .
.
- Czy
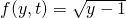 jest określona i ciągła w otoczeniu
jest określona i ciągła w otoczeniu 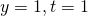 ?
? - Czy jej pochodna,
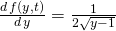 , też jest określona i ciągła w otoczeniu
, też jest określona i ciągła w otoczeniu 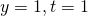 ?
? - Jak odpowiedź na powyższe punkty ma się do liczby rozwiązań poprzedniego zadania?
- Czy
- Co to jest, w kontekście równań różniczkowych:
- Efekt motyla
- Punkt stały
- Orbita
- Atraktor
Zadania
- Zapoznaj się z symulacją on-line atraktora Lorenza, http://www.malinc.se/m/Lorenz.php.
- Poeksperymentuj z parametrami układu równań.
- Jaki efekt ilustruje symulacja „niebieskich motyli” w „małym pudełku” (small cube)?
- Jaki efekt ilustruje symulacja „niebieskich motyli” w „dużym pudełku” (large cube)?
- Rozwiąż równania Lorenza
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{rcl} \displaystyle \frac{dx}{dt} & = & -\sigma x + \sigma y \\[1.85ex] \displaystyle \frac{dy}{dt} & = & -xz + rx -y \\[1.85ex] \displaystyle \frac{dz}{dt} & = & xy - bz \end{array}](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-9d2cecc32cb433d8e69aa32a3f3e88f4_l3.png)
dla parametrów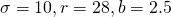 , z dowolnym warunkiem początkowym spełniającym
, z dowolnym warunkiem początkowym spełniającym 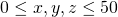 . W tym celu:
. W tym celu:
- Skopiuj do swojego katalogu roboczego plik lorenz.m:
function dx = lorenz (xx, t) dx = zeros(3,1); # rezerwacja miejsca global sigma; global r; global b; x = xx(1); # ułatwienie zapisu y = xx(2); z = xx(3); dx(1) = ... # uzupełnij dx(2) = ... # uzupełnij dx(3) = ... # uzupełnij endfunction
i uzupełnij w nim definicję funkcji lorenz (trzy wykropkowane instrukcje) zgodnie z definicją równania różniczkowego.
- Skopiuj do swojego katalogu roboczego plik make_lorenz.m:
global sigma; global r; global b ; sigma = ...; # uzupełnij r = ...; # uzupełnij b = ...; # uzupełnij x0 = ...; # uzupełnij y0 = ...; # uzupełnij z0 = ...; # uzupełnij N = 40000; t = linspace(0, 40, N); sol = lsode("lorenz", [x0, y0, z0], t); plot3(sol(1:N,1), sol(1:N,2), sol(1:N,3), "r", "linewidth", 2); xlabel("x", "fontsize", 15); ylabel("y", "fontsize", 15); zlabel("z", "fontsize", 15); set(gca, "fontsize", 16);i uzupełnij w nim wartości parametrów równania (
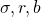 ) oraz warunku początkowego (
) oraz warunku początkowego (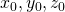 ) i uruchom ten skrypt. Porównaj kształt rozwiązania z tym, jak generuje program z zadania 1.
) i uruchom ten skrypt. Porównaj kształt rozwiązania z tym, jak generuje program z zadania 1. - Wygeneruj rozwiązania dla dwóch zupełnie różnych warunków początkowych, np. (1, 1, 1) i (20, -20, 10). Czy oba zbiegają do tego samego atraktora?
- Wygeneruj rozwiązania dla dwóch bardzo bliskich siebie warunków początkowych (
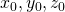 ), np. (1, 1, 1) oraz (1, 1, 1.000001).
), np. (1, 1, 1) oraz (1, 1, 1.000001).
- Zbadaj różnicę między oboma rozwiązaniami w funkcji czasu, np. instrukcją
plot(t, sol(:,1) - sol2(:,1));
- Lepszy sposób to wykres półlogarytmiczny:
semilogy(t, abs(sol(:,1) - sol2(:,1)));
- Zbadaj różnicę między oboma rozwiązaniami w funkcji czasu, np. instrukcją
- Skopiuj do swojego katalogu roboczego plik lorenz.m:
- (*) Zmiana prędkości pewnego samochodu od momentu wyłączenia silnika do chwili, w którym samochód się zatrzymuje, opisana jest równaniem
![Rendered by QuickLaTeX.com \[\displaystyle \frac{dv}{dt} = -(b + c \cdot v^2),\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-b78d861b2cdd13d576d147112cbae461_l3.png)
gdzie
 jest prędkością samochodu w metrach na sekundę, t – czasem wyrażonym w sekundach, b – współczynnikiem oporu dynamicznego, a c jest współczynnikiem oporu aerodynamicznego. Przyjmując
jest prędkością samochodu w metrach na sekundę, t – czasem wyrażonym w sekundach, b – współczynnikiem oporu dynamicznego, a c jest współczynnikiem oporu aerodynamicznego. Przyjmując 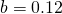 oraz
oraz 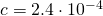 :
:- Oszacuj czas, po jakim samochód się zatrzyma oraz drogę, jaką zdoła przejechać, jeśli jego prędkość początkowa wynosi 100 km/h.
- O ile zmieniłby się czas i droga do zatrzymania samochodu, gdyby zaniedbać opór powietrza, przyjmując
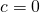 ?
?