MultiFun = Funkcje wielu zmiennych
Spis treści
Wykład
Khan Academy
Lekcje w Khan Academy uzupełniają zajęcia kursowe. Najważniejszą ich zaletą jest klarowność wywodu i koncentracja na kształtowaniu intuicji matematycznej. Przy okazji można doszlifować swój angielski.
Thinking about multivariable functions.
Quiz
W tym tygodniu niespodzianka. Oto przygotowany w Octave film ilustrujący drgania okrągłej idealnie sprężystej membrany:
Skrypt Octave, którego użyłem (zapisawszy go uprzednio w pliku animate.m), wygląda nastepująco:
graphics_toolkit ("gnuplot"); % eliminuje buga w linuksie w trybie GUI
set(0, 'defaultfigurevisible', 'off');
[x,y] = meshgrid([-1:0.01:1]);
S = 10; % S: gdzie obcinamy szereg?
% broot: pierwiastki funkcji bessela J0
broot = 14.9309 + pi*(-4:1:(S-4-1));
broot(1:4) = [2.4048, 5.5201, 8.6537, 11.7915];
r = sqrt(x.^2 + y.^2);
counter = -1; % licznik klatek filmu
for t = linspace (0, 2*pi, 1000) % 2*pi to niestety bledna hipoteza robocza
counter = counter + 1
z = x - x;
sum = z;
theta = 1./(r <= 1); % maska kola
for i=[1:S] % bierzemy S wyrazow szeregu
xi = broot(i);
coeff = 8/(xi^3 * besselj(1, xi)) * cos(xi*t);
sum = sum + coeff .* besselj(0, xi .* r);
end
z = theta .* sum; % gotowe z(x,y), czyli to, co wyswietlamy
surf(x,y,z);
hold on;
axis([-1 1 -1 1 -1.3 1.3]);
caxis([-1.3, 1.3]);
shading interp;
xlabel("x");
ylabel("y");
zlabel("u(x,y)");
tit = sprintf('t = %.3f', t/pi/0.85);
title(tit);
tt = 0:0.05:2*pi;
plot3(cos(tt), sin(tt), 0*tt, "k", "linewidth", 1);
hold off;
filename = sprintf('output/%d.png', counter);
#pause(0.01);
print (filename);
end
Powyższy program wyznacza położenie poszczególnych punktów membrany z gotowego rozwiązania (por. Równanie drgań membrany swobodnej/Membrana kołowa/Przykład):
![Rendered by QuickLaTeX.com \[u(r,t) = 8 \sum_{n=1}^\infty \frac{1}{x_n^3 \mathop{\mathrm{J}_1}(x_n)} \mathop{\mathrm{J}_0}(x_n r) \cos(x_n c t),\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-84f600051749317417cfe1aa40470b01_l3.png)
gdzie ![]() oznacza prędkość dźwięku w membranie, a
oznacza prędkość dźwięku w membranie, a ![]() to
to ![]() -ty pierwiastek funkcji Bessela
-ty pierwiastek funkcji Bessela ![]() . Wartości kilku pierwszych
. Wartości kilku pierwszych ![]() można odczytać np. ze strony MathWorld, a pozostałe oszacować wiedząc, że odległość między kolejnymi
można odczytać np. ze strony MathWorld, a pozostałe oszacować wiedząc, że odległość między kolejnymi ![]() dla dużych n dąży do
dla dużych n dąży do ![]() . Dobrą alternatywą są kalkulatory funkcji specjalnych lub wyznaczenie tych zer w
. Dobrą alternatywą są kalkulatory funkcji specjalnych lub wyznaczenie tych zer w Octave numerycznie, np. funkcją fsolve (ale to by zbytnio skomplikowało i zaciemniło program, mający mieć pewne walory demonstracyjne).
Powyższy program zakłada, że w bieżącym katalogu utworzono wcześniej podkatalog output. W linuksie można go uruchomić następująco:
> octave animate.m
Ponieważ jego wykonanie może zająć ponad pół godziny, alternatywnie można go uruchomić na serwerze (np. na pracowni studenckiej) w następujący sposób:
> nohup octave animate.m > qq &
i powrócić do serwera po mniej więcej godzinie, by utworzyć film. Ja w tym celu posłużyłem się komendą
> avconv -i %d.png oo.mp4
A teraz zadanie:
- Przedyskutujcie w grupie sens powyższego programu w Octave. Po co są poszczególne instrukcje? Które z instrukcji matematycznych działają na skalarach, a które w sposób wektorowy?
- Przedyskutujcie w grupie sposób implementacji w Octave powyżej przedstawionych wzorów matematycznych. Czy program usiłuje wyznaczyć dokładne wartości rozwiązania, a jeśli nie, to w którym miejscu to widać i dlaczego można tak zrobić?
Wskazówka: w mianowniku jest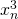 , przy czym
, przy czym 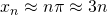 , a więc np.
, a więc np. 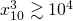 . Ponadto
. Ponadto 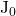 i
i 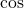 są funkcjami ograniczonymi.
są funkcjami ograniczonymi. - Czy dostrzegasz jakąś użyteczność funkcji specjalnych, np. użytych w tym przykładzie funkcji Bessela? Przedyskutuj ten problem.
- Przedyskutujcie w grupie instrukcje, które należy wykonać w linuksie, aby z klatek stworzyć film. Np. do czego służy polecenie
nohupi znaki>oraz&? Do czego służy avconv i co oznacza zapis-i %d.png? Z czym, znanym z programowania, kojarzy się%d?
Uwaga. Powyższy skrypt Octave nie działa w Windows ani w Linuksie Ubuntu 14.4 w wersji GUI, działa doskonale w wersji terminalowej; prawdopodobnie w Octave i/lub GhostScripcie jest błąd; skrypt działa wszędzie, jeśli usunie się w nim instrukcję print. Ja korzystałem z wersji terminalowej poprzez łącze ssh / putty. Wygenerowanie 1000 klatek filmu zajmuje na moim komputerze ok. 40 minut. Octave jest aplikacją jednowątkową i pełne wykorzystanie procesorów wielordzeniowych wymagałoby pewnej pomysłowości.
Uaktualnienie (13.01.2016). Kłopot z powyższym skryptem Octave w Linuksie pracującym w trybie GUI wynika z buga w bibliotece FLTK i/lub ze sposobu jej podpięcia pod Octave. Dopisałem na samym początku skryptu komendę graphics_toolkit ("gnuplot");, która wymusza użycie jako silnika graficznego biblioteki gnuplot. U mnie ta łatka całkowicie rozwiązuje problem.
Zadania
- Wykonaj rysunek funkcji
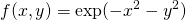 .
. - Narysuj elipsę jako krzywą parametryczną (może mieć osie skierowane wzdłuż osi x,y układu współrzędnych).
Wskazówka: zacznij od narysowania okręgu (było na wykładzie). - (*) Ogólne równanie krzywych stożkowych (okręgu, elipsy, paraboli i hiperboli) we współrzędnych biegunowych wygląda następująco:
![Rendered by QuickLaTeX.com \[r(\varphi) = \frac{l}{1 - e\cos \varphi},\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-182b3a21e29bb671ce6193e7b4f2c3ca_l3.png)
gdzie l i e są pewnymi (nieujemnymi) parametrami. Sprawdź, że dla
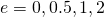 faktycznie otrzymuje się wykres okręgu, elipsy, paraboli i hiperboli. W ten sprytny sposób poćwiczysz posługiwanie się współrzędnymi biegunowymi.
faktycznie otrzymuje się wykres okręgu, elipsy, paraboli i hiperboli. W ten sprytny sposób poćwiczysz posługiwanie się współrzędnymi biegunowymi.