Wykład
Quiz
Quiz zawiera pytania, na które odpowiedź powinno się umieć podać z głowy.
- Na typowym wykresie y-x (współrzędne kartezjańskie) zmienną niezależną umieszcza się zwyczajowo na osi poziomej czy pionowej?
- Jeżeli f oznacza funkcję, to
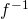 oznacza
oznacza 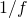 czy funkcję odwrotną do
czy funkcję odwrotną do 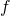 ?
? - Jeśli
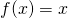 , to
, to 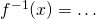
- Jeśli
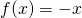 , to
, to 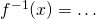
- Jeśli
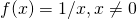 , to
, to 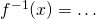
- Wykres funkcji odwrotnej do
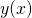 otrzymujemy, odbijając go względem prostej
otrzymujemy, odbijając go względem prostej 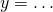
- Jeżeli
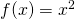 , to superpozycja f z samą sobą,
, to superpozycja f z samą sobą, 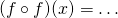
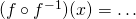
- Niech
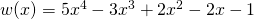
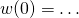
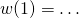
- Wyraz wolny tego wielomianu wynosi…
- Stopień tego wielomianu wynosi…
- Współczynnik liniowy równy jest w tym przypadku…
- O wielomianie
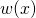 wiadomo, że jego wyraz wiodący ma postać
wiadomo, że jego wyraz wiodący ma postać 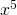 , a jego pierwiastkami są 1, 2, 3, 4 i 5. Co to za wielomian?
, a jego pierwiastkami są 1, 2, 3, 4 i 5. Co to za wielomian? - Faktoryzacja to przekształcenie wyrażenia do postaci iloczynu czy sumy?
- Czy różnica dwóch wielomianów stopnia n (np. 2) może być wielomianem niższego stopnia niż n?
- Czy suma dwóch wielomianów stopnia n (np. 2) może być wielomianem niższego stopnia niż n?
- Który z poniższych wielomianów na pewno ma pierwiastek rzeczywisty:
- Dowolny wielomian 3. stopnia
- Dowolny wielomian 6. stopnia
- Dowolny wielomian 2015 stopnia.
- Jaki wielomian definiuje w Octave instrukcja:
>> w = [3, -2, 0, 1];
Zadania
- Zdefiniuj w Octave dwa wielomiany,
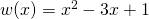 oraz
oraz 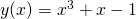 . Następnie:
. Następnie:
- Znajdź wszystkie pierwiastki rzeczywiste
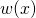
- Znajdź wszystkie pierwiastki rzeczywiste
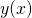
- Wyznacz iloczyn
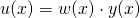
- Czy
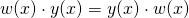 ?
? - Jak stopień
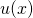 ma się do stopni
ma się do stopni 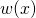 i
i 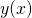 ?
? - Znajdź wszystkie pierwiastki rzeczywiste
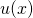 i porównaj je z pierwiastkami rzeczywistymi
i porównaj je z pierwiastkami rzeczywistymi 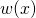 oraz
oraz 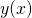 .
. - Czy odpowiedzi na pytania d-f mają, Twoim zdaniem, charakter uniwersalny?
- Narysuj wykres
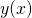 dla
dla 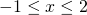 .
. - Wykonaj ciąg powiększeń wykresu w pobliżu jego miejsca zerowego. Czy w kolejnych powiększeniach wykres zaczyna przypominać fragment linii prostej?
- Znajdź wszystkie pierwiastki rzeczywiste
- Wykres funkcji
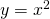 dla
dla 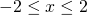 można w Octave utworzyć następująco:
można w Octave utworzyć następująco:
N = 100; x = linspace(-2, 2, N); y = x .* x; plot(x, y);
W jaki sposób, mając
xiy, wygenerować wykres „funkcji odwrotnej” (i dlaczego w poleceniu użyłem cudzysłowu)? - Za pomocą metody z poprzedniego zadania:
- narysuj wykres funkcji odwrotnej do
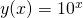 i sprawdź, czy pokrywa się on z wykresem funkcji logarytmicznej
i sprawdź, czy pokrywa się on z wykresem funkcji logarytmicznej y(x) = log10(x) - narysuj wykres funkcji odwrotnej do
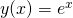 i sprawdź, czy pokrywa się on z wykresem funkcji logarytmicznej
i sprawdź, czy pokrywa się on z wykresem funkcji logarytmicznej y(x) = log(x)(W Octavelog(x)oznacza logarytm naturalny zx) - narysuj wykres funkcji odwrotnej do
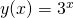 i sprawdź, czy pokrywa się on z wykresem funkcji logarytmicznej
i sprawdź, czy pokrywa się on z wykresem funkcji logarytmicznej y(x) = log(x)/log(3). Czy pamiętasz jeszcze wzór na zamianę podstawy logarytmów?
- narysuj wykres funkcji odwrotnej do
- W Octave istnieje możliwość definiowania funkcji anonimowych – w pojedynczym wierszu, bez pomocy słów kluczowych
functioniendfunction. Służy do tego operator@. Na przykład, aby zdefiniować funkcję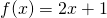 oraz
oraz 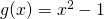 , można posłużyć się dwoma instrukcjami:
, można posłużyć się dwoma instrukcjami:
f = @(x) 2 * x + 1; g = @(x) x .* x - 1;
Skorzystaj z powyższego przykładu, by wyświetlić na jednym rysunku wykresy funkcji
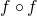 ,
, 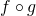 ,
, 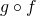 i
i 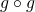 dla
dla 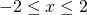 .
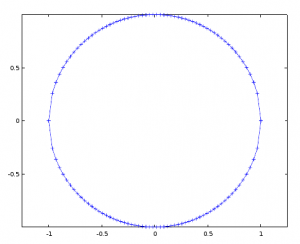
. - Poniższy kod generuje wykres okręgu o promieniu 1:
N = 60; f = @(x) sqrt(1 - x.* x); x = linspace(-1, 1, N); x0 = linspace(1, -1, N); y = [f(x), -f(x0)]; x = [x, x0]; plot (x, y, "+-"); axis("equal");Kod ten ma pewną wadę: punkty nie układają się równomiernie na okręgu, co prowadzi do zniekształcenia kształtu okręgu w okolicach osi x, por. rysunek po lewej:
- Wstępna wersja rysunku
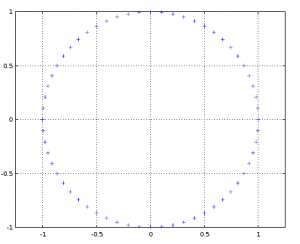
- Wersja docelowa
-
- Do czego służą nawiasy kwadratowe w instrukcji
x = [x, x0];? - Zaproponuj inny sposób narysowania okręgu, który będzie gwarantował równomierny rozkład punktów, jak na rysunku po prawej. Jako zmiennej niezależnej możesz użyć kąta
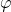 oraz podstawień
oraz podstawień 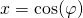 i
i  .
.
- Do czego służą nawiasy kwadratowe w instrukcji
Uwaga: zwróć uwagę na to, że w powyższy sposób można w Octave rysować szersze klasy obiektów niż wykresy funkcji.
- (*) Niech
x = [9, 4, 11, 36, 85, 164, 279, 436, 641, 900]. Wyrazy tego ciągu zostały wygenerowane za pomocą pewnego wielomianu niewielkiego stopnia, tj.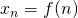 dla
dla 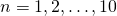 , przy czym
, przy czym 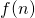 jest wielomianem zmiennej
jest wielomianem zmiennej 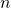 . Pytanie brzmi: jaki to wielomian? Aby na nie odpowiedzieć
. Pytanie brzmi: jaki to wielomian? Aby na nie odpowiedzieć
- zapoznaj się z dokumentacją funkcji
polyfit. - wykonaj odpowiednie obliczenia, używając
polyfit.
- zapoznaj się z dokumentacją funkcji