Wykład
Quiz
- Znajdź błąd w następującym rozumowaniu:
- Jeżeli funkcja ciągła przyjmuje w punktach a i b wartości f(a) i f(b), to przyjmuje też wszystkie wartości pomiędzy f(a) i f(b).
- Funkcja
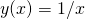 jest funkcją elementarną, a więc jest funkcją ciągłą; ponadto y(-1) = -1 oraz y(1) = 1.
jest funkcją elementarną, a więc jest funkcją ciągłą; ponadto y(-1) = -1 oraz y(1) = 1. - Łącząc powyższe fakty dochodzimy do wniosku, że musi istnieć liczba
![Rendered by QuickLaTeX.com x_0\in[-1,1]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-d02b5397eaa1fb8ce40160c30cf4970e_l3.png) taka, że
taka, że 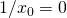 .
.
- Czy funkcja, której wykres przedstawia poniższy rysunek

- ma granicę lewostronną w
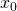 ?
? - ma granicę prawostronną w
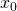 ?
? - jest ciągła lewostronnie w
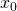 ?
? - jest ciągła prawostronnie w
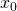 ?
? - jest ciągła w
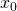 ?
?
- ma granicę lewostronną w
- Czy funkcja
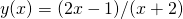 , której wykres przedstawia poniższy rysunek
, której wykres przedstawia poniższy rysunek

- ma w punkcie x = -2 granicę prawostronną, właściwą lub nie?
- ma w punkcie x = -2 granicę lewostronną, właściwą lub nie?
- jest w punkcie x = -2 lewostronnie lub prawostronnie ciągła?
- jest w punkcie x = -2 ciągła?
- jest ciągła na odcinku [1,2]?
- jest ciągła na odcinku [-3, 0]?
- Na podstawie wykresu funkcji z poprzedniego pytania odpowiedz na następujące pytania:
- Czy funkcja ta ma funkcję odwrotną?
- Jeśli tak, to jaka jest jej dziedzina?
- Czy ta funkcja odwrotna jest w swej dziedzinie ciągła?
- O pewnym wielomianie
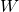 wiadomo, że
wiadomo, że 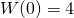 i
i 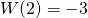 . Czy ten wielomian musi mieć pierwiastek?
. Czy ten wielomian musi mieć pierwiastek? - Skoro
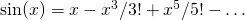 , to ile wynosi
, to ile wynosi
![Rendered by QuickLaTeX.com \[\lim_{x\to 0} \frac{\sin(x)}{x}\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-40868d0cd3e9753f2703ea2d603ac5ca_l3.png)
- Skoro
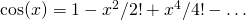 , to ile wynosi
, to ile wynosi
![Rendered by QuickLaTeX.com \[\lim_{x\to 0} \frac{1 - \cos(x)}{x^2}\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-41f390ce0863f1b1498f50c8f436948f_l3.png)
- Skoro
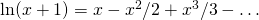 , to ile wynosi
, to ile wynosi
![Rendered by QuickLaTeX.com \[\lim_{x\to 0} \frac{\ln(x+1)}{x}\]](http://users.ift.uni.wroc.pl/~zkoza/matematyka/wp-content/ql-cache/quicklatex.com-e6e141209d5e25d51e9a422fbf8156aa_l3.png)
Zadania
- Jak już wiesz,
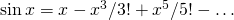 , natomiast
, natomiast 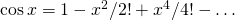 . Niech
. Niech 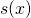 będzie wielomianem, który powstaje z powyższego szeregu dla
będzie wielomianem, który powstaje z powyższego szeregu dla 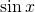 po odrzuceniu wyrazów w potędze wyższej niż 5. Podobnie niech c(x) będzie wielomianem, który powstaje z szeregu dla
po odrzuceniu wyrazów w potędze wyższej niż 5. Podobnie niech c(x) będzie wielomianem, który powstaje z szeregu dla 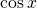 po odrzuceniu wyrazów wyższego stopnia niż 5.
po odrzuceniu wyrazów wyższego stopnia niż 5.
- Utwórz iloczyn
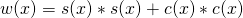 , który powinien w przybliżeniu równać się
, który powinien w przybliżeniu równać się 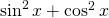 , czyli mieć wartość 1. Uwaga. jeżeli używasz Octave i polecenia
, czyli mieć wartość 1. Uwaga. jeżeli używasz Octave i polecenia conv, to pamiętaj, że oba wielomiany muszą mieć dokładnie ten sam stopień. - Sprawdź, że wyraz wolny
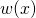 faktycznie równa się 1, a wszystkie pozostałe jego wyrazy stopnia ≤ 5 równe są 0.
faktycznie równa się 1, a wszystkie pozostałe jego wyrazy stopnia ≤ 5 równe są 0. - Sprawdź, jakie wartości ma
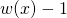 dla
dla x = linspace(0, pi, 8).
- Utwórz iloczyn
- Niech
x = 0:0.1:3iy = exp(x)(Octave).- Za pomocą polecenia
polyfitdopasuj do (x,y) wielomiany stopnia od 1 do 5. Czy współczynniki tych wielomianów w wyrazach o potędze ≤ 3 dążą do współczynników wielomianu uzyskanego z rozwinięcia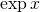 w szereg względem 0, tj.
w szereg względem 0, tj. 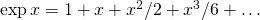 ?
?
Wskazówka. Szybka komenda do wyświetlenia jednego z tych wielomianów:polyout(polyfit(x, y, 1));
- Wyświetl
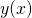 oraz kolejne wielomiany aproksymacyjne otrzymane w poprzednim punkcie. Czy wykresy wielomianów wyższych stopni coraz lepiej odpowiadają aproksymowanej funkcji na zadanym przedziale?
oraz kolejne wielomiany aproksymacyjne otrzymane w poprzednim punkcie. Czy wykresy wielomianów wyższych stopni coraz lepiej odpowiadają aproksymowanej funkcji na zadanym przedziale?
Wskazówka:plot(x, polyval(polyfit(x, yy, 1), x), "+", x, y);
- Za pomocą polecenia