PDE – Matematyka dla ISSP

PDE (ang. Partial Differential Equations) to angielski skrótowiec oznaczający „równania różniczkowe cząstkowe”.

Wykład

Zadania

1. Oblicz różniczkę df dla:
  1. $f(x,y,z) = x^2 + y*z$
  2. $f(x,y,z) = z\ln(xy)$
  3. $f(x,y) = \frac{x}{y}$
2. Przepisz równania używając u=u(x,t) oraz pochodnych w jawnej postaci czyli \partial u/\partial t =u_t, \partial u/\partial x =u_x, \partial^2 u/\partial t^2 =u_{tt}, \partial^2 u/\partial t \partial x =u_{tx}, itd:
  1. $\displaystyle u_{t}+u_{x}+uu_{x}-u_{xxt}=0$
  2. $\displaystyle u_{t}=u^{3}u_{xxx}.\,$
  3. $\displaystyle (1-u_{t}^{2})u_{xx}+2u_{x}u_{t}u_{xt}-(1+u_{x}^{2})u_{tt}=0$
3. Sprawdź czy funkcja $\psi(t,x)=A*cos(\omega t + k x)$ , jest rozwiązaniem równania różniczkowego cząstkowego (tzw. “falowego”) $\frac{\partial^2 \psi(t,x)}{\partial t^2}-V^2\frac{\partial^2 \psi(t,x)}{\partial x^2}=0$ , gdzie $V=\frac{\omega}{k} =\frac{\frac{2\pi}{T}}{\frac{2\pi}{\lambda}}$ . Jakie warunki brzegowe możemy w tym przypadku zapisać w chwili t=0?
4. Korzystając z prawa Ohma, $R=U/I$ , wyznacz opór elektryczny $R$ i oszacuj błąd pomiaru tej wielkości, jeżeli $U=10.0$ V, $\Delta U = 0.1$ V, $I = 5$ A, a $\Delta I = 0.05$ A.

Dodatkowe zadania

Symbol \partial używany bywa na oznaczenie brzegu jakiegoś obszaru. Co oznacza
1. $\partial V$ , jeżeli $V$ jest kulą o promieniu 1 i środku w $(0,0,0)$ (figura przestrzenna)?
2. $\partial S$ , jeżeli $S$ jest kwadratem o boku 2 i środku w $(0,0)$ (figura płaska)?
Podaj wartość dowolnego (niezerowego) wektora prostopadłego do:
1. prostej $3x - 4y = 9$
2. prostej $y = 2x - 1$
3. płaszczyzny $3x+2y+z=1$
4. płaszczyzny $z=x+y$ Podpowiedź: sprawdź wykład i kwestię liczenia wektorów z pochodnych cząstkowych na równanie prostej.
Podaj wartość wektora normalnego do płaszczyzny $x+2y +2z = 0$ (zwrot dowolny).
Wyznacz równanie płaszczyzny stycznej do paraboloidy $z(x,y)=x^2+2y^2$ w punkcie $x=1,y=1,z=3$ .
Wyznacz kierunek wektora prostopadłego do paraboloidy $z=x^2+2y^2$ w punkcie $x=1,y=1,z=3$ .
Poniższy rysunek przedstawia wykres funkcji z(x,y) = 2-x^2-y^2-x.

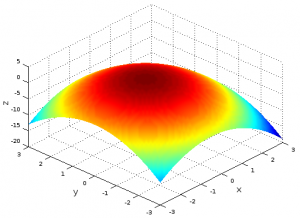
Gdzie znajduje się maksimum tej funkcji? Aby odpowiedzieć na to pytanie:
1. Zastanów się, czy płaszczyzna styczna do wykresu funkcji w jej punkcie ekstremalnym musi być równoległa do płaszczyzny x-y (czyli prostopadła do osi z)?
2. Jak wygląda postać ogólnego równania płaszczyzny prostopadłej do osi z?
3. Korzystając z faktu, że równanie płaszczyzny stycznej do wykresu funkcji różniczkowalnej $f$ ma postać $z-z_0 = \frac{\partial f}{\partial x} (x-x_0) + \frac{\partial f}{\partial y} (y-y_0)$ , a wektor prostopadły do tej płaszczyzny ma postać $(-\frac{\partial f}{\partial x}, -\frac{\partial f}{\partial y}, 1)$ , wykaż, że w punkcie ekstremalnym zachodzi $\frac{\partial f}{\partial x} = 0, \frac{\partial f}{\partial y} = 0.$
4. Korzystając z powyższego wzoru znajdź położenie maksimum tej funkcji.
Czy na mapie konturowej obszary, w których poziomice się do siebie zbliżają, charakteryzują się dużym czy małym gradientem wzniesienia terenu? W jaki sposób oszacować na mapie konturowej kierunek nachylenia terenu?
Temperatura metalowego pręta ma postać $T(x) = 120 + 0.1x, 0\le x \le 100$ , gdzie x jest odległością od początku pręta w centymetrach, a $T$ – temperaturą w stopniach Celsjusza. Ile wynosi gradient temperatury? W którą stronę płynie ciepło?
Typowy gradient temperatury w skorupie ziemskiej w Polsce wynosi ok. 33°C/km.
1. Oszacuj temperaturę panującą na dole odwiertu o głębokości 3 km służącego do eksploatacji złóż gazu łupkowego.
2. Jaka temperatura panowałaby w takim odwiercie wykonanym w Islandii, gdzie gradient temperatury wynosi ok. 100°C/km?
Zajrzyj na stronę Wikipedii Operator nabla w różnych układach współrzędnych. W zamieszczonej tam tabeli odnajdź postać gradientu we współrzędnych sferycznych. Na tej podstawie zdecyduj, czy do wyznaczenia gradientu temperatury (T) wewnątrz Słońca potrzeba stosować jakieś specjalne przeliczniki/współczynniki/wagi, czy też można po prostu wyznaczyć $\partial T(r)/\partial r$ .
Temperatura jądra Słońca szacowana jest na 1,6 ×10⁷ K, a temperatura jego fotosfery (“powierzchni”) to ok. 5800 K. Wiedząc, że promień Słońca to ok. 700 000 km, oszacuj gradient temperatury w Słońcu. W jakim kierunku płynie ciepło?
Czy wektory (1,2,5) i (-5,5,-1) są do siebie prostopadłe?
Przyporządkuj równaniom odpowiedni opis:
1. 1. $\vec\nabla \times \vec{E} = -\frac{\partial \vec{B}} {\partial {t}}$
  2. $\vec\nabla \times \vec{B} = \mu \vec{j} +\mu \varepsilon \frac{\partial \vec{E}} {\partial {t}}$
  3. $\varepsilon \vec\nabla \cdot \vec{E} = \rho$
  4. $\vec\nabla \cdot \vec{B} = 0$
  5. $\frac{\partial T}{\partial t} = \kappa \nabla^2 T$
  6. $\vec{\nabla } \cdot \vec{u} =0$
  7. $\frac{\partial \rho}{\partial t} = \vec{\nabla} \cdot (\rho \vec{u})$
Opisy równań:
A) Prawo zachowania masy (dynamika płynów)
B) Źródłem pola elektrycznego są ładunki elektryczne
C) Przepływający prąd oraz zmienne pole elektryczne wytwarzają pole magnetyczne
D) Nie istnieją ładunki magnetyczne
E) Prędkość zmiany temperatury jest proporcjonalna do nadwyżki średniej temperatury w otoczeniu danego punktu względem temperatury w tym punkcie
F) Zmienne w czasie pole magnetyczne wytwarza pole elektryczne
G) Przepływ jest nieściśliwy