ODE

Wykład

• Prezentacja
• Klasyfikacja: liniowe i nieliniowe
• Notatki svg+ Prezentacja stara
• Khan Academy: Wstęp do równań różniczkowych

Zadania

1. Jaki jest rząd następujących równań różniczkowych zwyczajnych:
   1.   \frac{dx}{dt} = x^2
   2.   \left(\frac{dx}{dt}\right)^2 = x
   3.   \frac{d^2x}{dt^2} = \left(\frac{dx}{dt}\right)^3
   4.   x +  \frac{dx}{dt} \cdot \frac{d^2 x}{dt^2} = 0
2. Jak wygląda rozwiązanie ogólne równań postaci
   \frac{dx}{dt} = f(t)
3. Rozwiąż równania różniczkowe pierwszego rzędu:
   a. \frac{d y}{dx}=\frac{x}{y}
   b. \frac{d y}{dx}=\frac{y}{x}
   c. \frac{d y}{dx}=\frac{1}{x}
   d. \frac{d y}{dx}=xy
   e. \frac{d y}{dx}=\sqrt{x}
   f. ydx+xdy=0
4. Rozwiąż równania różniczkowe drugiego rzędu:
   a. \frac{d^2 x}{dt^2}-a=0
   b. \frac{d^2 y}{dx^2}-\frac{d y}{dx}=0
   c. y''+y'=0, przy warunkach brzegowych y(0)=2 oraz y'(0)=-1
   d. y''-y=0, przy warunkach brzegowych y(0)=2 oraz y'(0)=0
   e. \frac{d^2 y}{dx^2}=\omega^2 y
   f. \frac{d^2 y}{dx^2}=-\omega^2 y

Dodatkowe zadania

1. Co to jest, w kontekście równań różniczkowych:
   1. Efekt motyla
   2. Punkt stały
   3. Orbita
   4. Atraktor
2. Zmiana prędkości pewnego samochodu od momentu wyłączenia silnika do chwili, w którym samochód się zatrzymuje, opisana jest równaniem
   \frac{dv}{dt} = -(b + c \cdot v^2),
   gdzie v jest prędkością samochodu w metrach na sekundę,  t – czasem wyrażonym w sekundach, b – współczynnikiem oporu dynamicznego, a c jest współczynnikiem oporu aerodynamicznego. Przyjmując b=0.12 oraz c=2.4\cdot 10^{-4}:
   1. Oszacuj czas, po jakim samochód się zatrzyma oraz drogę, jaką zdoła przejechać, jeśli jego prędkość początkowa wynosi 100 km/h.
   2. O ile zmieniłby się czas i droga do zatrzymania samochodu, gdyby zaniedbać opór powietrza, przyjmując c=0?
3. Przyporządkuj pola kierunków odpowiednim równaniom:
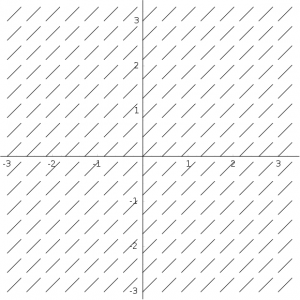   a. \frac{dx}{dt} = 1,
   b. \frac{dx}{dt} = t ,
   c. \frac{dx}{dt} = t x
4.  Zapoznaj się z symulacją on-line atraktora Lorenza, http://www.malinc.se/m/Lorenz.php.
   • Poeksperymentuj z parametrami układu równań.
   • Jaki efekt ilustruje symulacja “niebieskich motyli” w “małym pudełku” (small cube)?
   • Jaki efekt ilustruje symulacja “niebieskich motyli” w “dużym pudełku” (large cube)?
5. Rozwiąż równania Lorenza
   \begin{array}{rcl} \displaystyle \frac{dx}{dt} & = & -\sigma x + \sigma y \\[1.85ex] \displaystyle \frac{dy}{dt} & = & -xz + rx -y \\[1.85ex] \displaystyle \frac{dz}{dt} & = &  xy - bz \end{array}
   dla parametrów \sigma = 10, r=28, b = 2.5, z dowolnym warunkiem początkowym spełniającym 0 \le x,y,z \le 50. W tym celu:
   1. Skopiuj do swojego katalogu roboczego plik lorenz.m:

      function dx = lorenz (xx, t)
        dx = zeros(3,1);  # rezerwacja miejsca
        global sigma;
        global r;
        global b;
        x = xx(1);   # ułatwienie zapisu
        y = xx(2);
        z = xx(3);
        dx(1) = ... # uzupełnij
        dx(2) = ... # uzupełnij
        dx(3) = ... # uzupełnij
      endfunction

      i uzupełnij w nim definicję funkcji lorenz (trzy wykropkowane instrukcje) zgodnie z definicją równania różniczkowego.

   2. Skopiuj do swojego katalogu roboczego plik make_lorenz.m:

      global sigma;
      global r;   
      global b ;     
      sigma = ...; # uzupełnij
      r = ...; # uzupełnij
      b = ...; # uzupełnij
      
      x0 = ...;  # uzupełnij 
      y0 = ...;  # uzupełnij
      z0 = ...;  # uzupełnij
      
      N = 40000;
      t = linspace(0, 40, N);
      sol = lsode("lorenz", [x0, y0, z0], t);
      
      plot3(sol(1:N,1), sol(1:N,2), sol(1:N,3), "r", "linewidth", 2);
      xlabel("x", "fontsize", 15);
      ylabel("y", "fontsize", 15);
      zlabel("z", "fontsize", 15);
      set(gca, "fontsize", 16);
      

      i uzupełnij w nim wartości parametrów równania (\sigma, r, b) oraz warunku początkowego (x_0, y_0, z_0) i uruchom ten skrypt. Porównaj kształt rozwiązania z tym, jak generuje program z zadania 1.

   3. Wygeneruj rozwiązania dla dwóch zupełnie różnych warunków początkowych, np. (1, 1, 1) i (20, -20, 10). Czy oba zbiegają do tego samego atraktora?
   4. Wygeneruj rozwiązania dla dwóch bardzo bliskich siebie warunków początkowych (x_0, y_0, z_0), np. (1, 1, 1) oraz (1, 1, 1.000001).
      • Zbadaj różnicę między oboma rozwiązaniami w funkcji czasu, np. instrukcją

        plot(t, sol(:,1) - sol2(:,1));

      • Lepszy sposób to wykres półlogarytmiczny:

        semilogy(t, abs(sol(:,1) - sol2(:,1)));