Pochodna (2) – Matematyka dla ISSP

Wykład

Druga część wykładu o pochodnych.

Zadania do wykonania ręcznie

Powiąż wykresy prędkości z wykresami przyspieszeń:
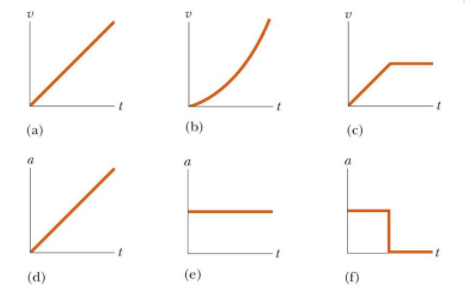
Narysuj wykres położenia od czasu i przyspieszenia od czasu:
Narysuj wykresy prędkości od czasu i przyspieszenia od czasu:
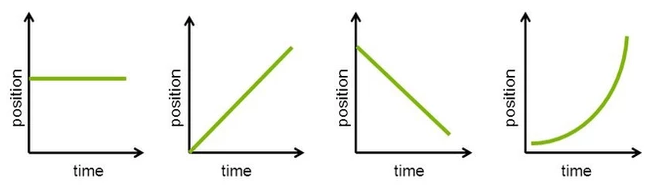
Narysuj wykres położenia od czasu wiedząc, że
Narysuj wykres prędkości od czasu wiedząc, że
Jeżeli małpka na sprężynie

porusza się wzdłuż jednej prostej, np. w kierunku góra-dół, to w punktach maksymalnego wychylenia jej prędkość znika. Jak ta obserwacja ma się do sposobu ustalania ekstremów funkcji za pomocą pochodnych?
Rozpatrzmy funkcję y(x) = \sqrt{1+x}.
- Znajdź równanie prostej, która aproksymuje tę funkcję w pobliżu punktu $x=0$ .
- Uzasadnij, że dla dostatecznie małych $x$ wartość wyrażenia $\sqrt{1+x}$ można przybliżyć wyrażeniem $1+x/2$ . Uwaga: jest to tak często używane przybliżenie, że warto je zapamiętać.
- Oszacuj w pamięci wartość wyrażeń $\sqrt{1.02}$ oraz $\sqrt{0.96}$ .
Rozwiń funkcję $sin(x)$ w szereg Taylora w punkcie $x_0=\pi$ .
Rozwiń funkcję $sin(x)$ w szereg Taylora w punkcie $x_0=3\pi/2$ .
Policz pochodną z $e^{ax}$ z definicji ilorazu różnicowego. Wskazówka: w którymś momencie musisz użyć rozwinięcia $e^{ax}$ w szereg Taylora.
Policz styczną w punkcie x_0=1:
- funkcji $\frac{1}{x}$
- funkcji $x\cdot sin(x^2)$ .
Niech y = k\sin(ax). Oblicz:
- $\frac{d\,y}{d\,x}$
- $\frac{d\,y}{d\,a}$
- $\frac{d\,y}{d\,k}$
Podaj różniczki następujących funkcji jednej zmiennej:
- $y(x) = \sin(2x)$
- $y(x) = \ln (3x)$
- $y(t) = 4\exp(-3t)$
- $y(t) = g\,t^2/2 + v_0\,t$
- $x(t) = \sin(a\,t)\exp(-\omega\,t)$
Podaj różniczki następujących funkcji dwóch zmiennych (pamiętaj, że w takim przypadku wzór na różniczkę zawiera tzw. pochodne cząstkowe, z “de kręcone”):
- $\psi(t,x) = \sin(k\,x)\exp(-\omega\,t)$
- $f(x,y) = x/y$
Pomiar średnicy pewnego koła dał wartość L = 31.0 \pm 0.5 cm. Na tej podstawie oszacowano, że obwód tego koła wynosi O = \pi L \approx 97.4 \;\mathrm{cm}, a jego pole to P = \frac{\pi L^2}{4} \approx 754.8 \;\mathrm{cm}^2. Oszacuj niepewność pomiaru:
- długości obwodu tego koła, $\Delta O$
- pola powierzchni tego koła, $\Delta P$ .
Gdyby średnica koła wzrosła 2 razy, to jego obwód również wzrósłby 2 razy, natomiast pole jego powierzchni powiększyłoby się 4 razy. Przypuśćmy, że niepewność pomiarową długości średnicy koła uda się zredukować o 50%. Jak wpłynie to na zmianę niepewności pomiarowej:
- obwodu koła, $\Delta O$ ?
- pola powierzchni koła, $\Delta P$ ?
Korzystając z prawa Ohma, $R=U/I$ , wyznacz opór elektryczny $R$ i oszacuj błąd pomiaru tej wielkości, jeżeli $U=10.00$ V, $\Delta U = 0.10$ V, $I = 5.00$ A, a $\Delta I = 0.05$ A.

Zadania do wykonania przy asyście komputera

Wyznacz komputerowo ekstremum funkcji:
- $x^x$
- $x^{-x}$
- $x^3 - 3x^2 + 4$
- $e^x - 2x^2$

Przeanalizuj kod pod poniżej rysujący funkcję i pochodną, wybierz jakąś inną skomplikowaną funkcję, sprawdź na wykresie czy zerowanie pochodnej wskazuje punkt ekstremum lub też punkt przegięcia:

% Define the function and numerical derivative
f = @(x) x.^2; % Function
numerical_derivative = @(f, x, dx) (f(x + dx) - f(x)) ./ dx; % Numerical derivative

% Parameters
dx = 0.0001; % Small step size
x_values = linspace(-10, 10, 500); % Generate x values
f_values = f(x_values); % Calculate function values
derivative_values = numerical_derivative(f, x_values, dx); % Calculate derivative values

% Plot the function and its derivative
figure;
hold on;

% Plot f(x)
plot(x_values, f_values, 'b-', 'LineWidth', 2, 'DisplayName', 'f(x) = x^2');

% Plot f'(x)
plot(x_values, derivative_values, 'r--', 'LineWidth', 2, 'DisplayName', 'f''(x) = 2x');

% Labels and Legend
title('Function and its Derivative', 'FontSize', 16);
xlabel('x', 'FontSize', 14);
ylabel('y', 'FontSize', 14);
legend('show', 'Location', 'northwest');

% Ensure the same ratio of axes
axis equal;
grid on;

hold off;

Zbadaj właściwości funkcji
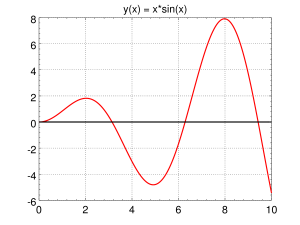
y(t) = t\sin(t),
dla 0 \le t \le 10.
Zadanie może wydawać się żmudne, ale w rzeczywistości jest to dość proste ćwiczenie na (a) rysowanie wykresów w Octavie i (b) korzystanie z funkcji fzero. Jeśli wydaje się zbyt trudne, można je rozwiązywać w parach. Poniżej animacja tej funkcji, a tutaj jest link do skryptu gnuplota generującego tę animację.

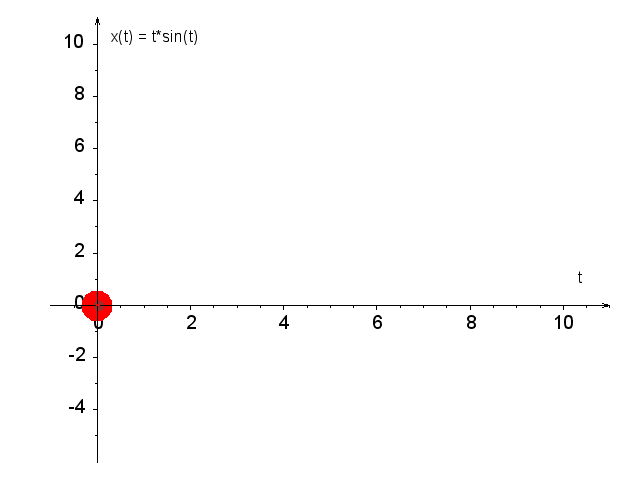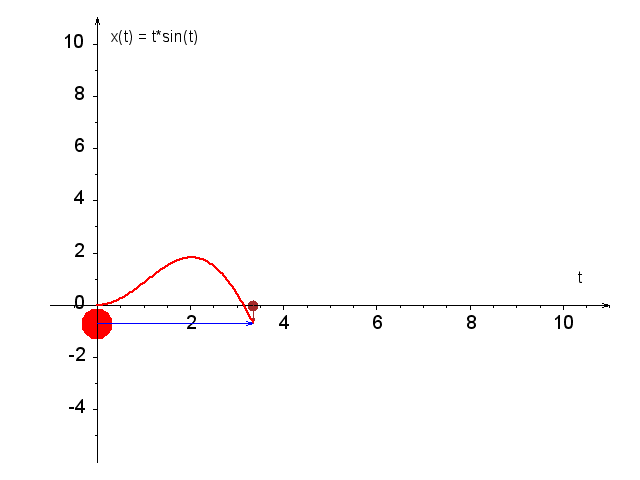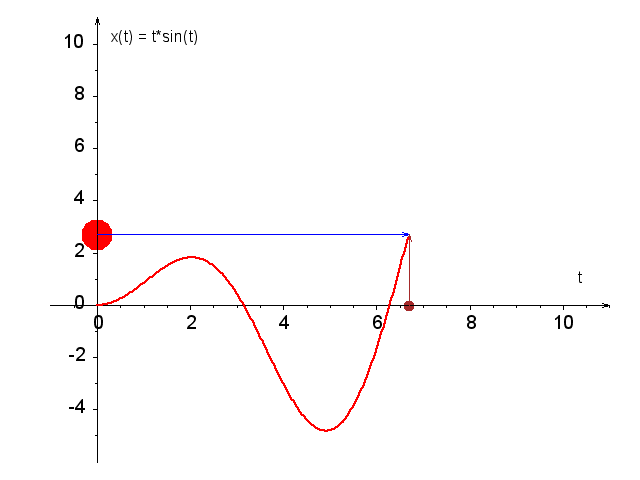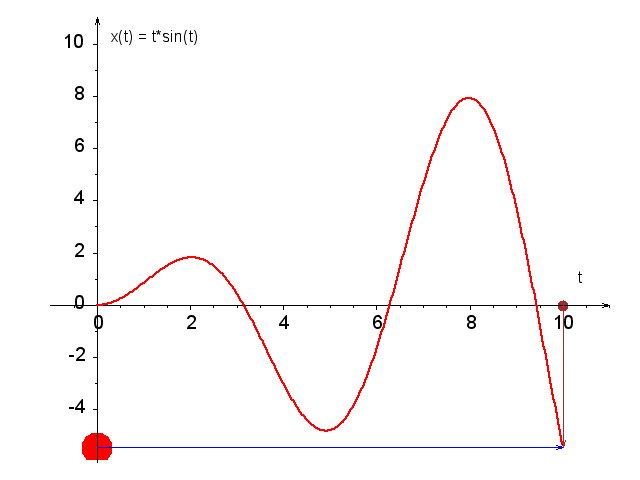
Plan działania do zad. 2:
1. Zrób wykres tej funkcji dla 0 \le t \le 10. Aby uzyskać czytelny wykres, możesz użyć następującego ciągu instrukcji:
```
N = 1001; 
tmax = 10;
t = linspace(0, tmax, N);
x = @(t) (t .* sin(t));
# v = @(t) (...);   # <-- odkomentuj i uzupełnij później
# a = @(t) (...);   # <-- odkomentuj i uzupełnij później
fig = plot(t, x(t), "-r", t, 0*t, "-k");
ax = gca();      # uchwyt do opisu osi
leg = legend();  # uchwyt do legendy wykresu 
set (ax, "fontsize", 20);
set (ax, "xminortick", "on");
set (ax, "yminortick", "on");
set (leg, "fontsize", 20);
set (fig, "linewidth", 2);
title("y(t) = t*sin(t)");
grid on;
```
  Wykres powinien wyglądać mniej więcej tak:
2. Na podstawie rysunku oszacuj, ile ta funkcja ma miejsc zerowych, maksimów, minimów i punktów przegięcia na przedziale $0\le t \le 10$ .
3. Na podstawie rysunku oszacuj, dla jakich wartości $t$ funkcja $x(t)$ jest rosnąca, malejąca, wklęsła, wypukła.
4. Miejsca zerowe uzyskujemy z rozwiązania równania $t\cdot \sin t = 0$ , czyli $t=0$ lub $\sin t = 0$ , czyli $t = 0, \pi, 2\pi, 3\pi$ .
5. Czy miejsca zerowe można łatwo odczytać z wykresu? W instrukcji plot dodaj parametr “+”:
```
fig = plot(x, y(x), "-+r", x, 0*x, "-k");
```
  tak, aby na wykresie pojawiły się punkty. Powiększ wykres wokół drugiego miejsca zerowego (o wartości $\pi$ ). W systemie Windows wystarczy wybrać narzędzie zoom (z+) i kilkukrotnie kliknąć okolice domniemanego punktu zerowego. Daje to następujący efekt:
  
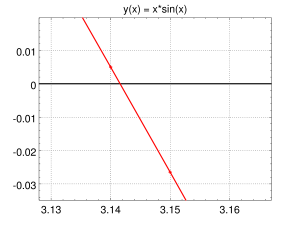
  Należy zauważyć, że Octave rysuje wykres składający się z odcinków, które łączą punkty wykresu, jest więc przybliżoną reprezentacją rzeczywistego wykresu. Jeśli składowe “x” punktów wykresu oddalone są od siebie o 0.01, jak na rysunku powyżej, to z jaką dokładnością odcinek aproksymuje krzywą? Można oczekiwać, że ta dokładność jest rzędu $h^2$ , gdzie $h$ to połowa odległości między składowymi “x” punktów. W naszym przypadku jest to $h^2=0.000025$ . W rzeczywistości dokładność tej metody jest rzędu $0.00001$ , czyli sześć cyfr znaczących, co ilustruje poniższy rysunek, na którym kolorem niebieskim zaznaczono znacznie dokładniejszy przebieg krzywej $x(t)$ :
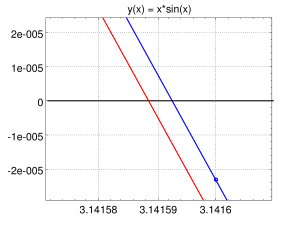
6. Położenia miejsc zerowych dowolnej funkcji łatwo wyznaczyć w Octave za pomocą funkcji fzero:
```
>> fzero (y, 3)
ans = 3.14159265358980
```
  w której pierwszym argumentem jest funkcja, a drugim – przybliżona wartość poszukiwanego miejsca zerowego. Za pomocą tej funkcji znajdź kolejne miejsca zerowe funkcji $x(t) = t\sin t$ w przedziale $0 \le t \le 10$ i sprawdź, że rzeczywiście równe są $0, \pi, 2\pi$ i $3\pi$ .
7. Skoro znamy już punkty zerowe funkcji x(t), czas na wyznaczenie ekstremów, czyli minimów i maksimów. Najprostsze podejście polega na powiększaniu wykresu w okolicach punktu, w których spodziewamy się występowania minimum lub maksimum:
  
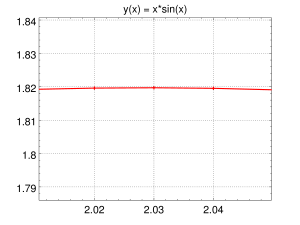
  Jak widać, ta metoda nie pozwala oszacować (w Octave) położenia maksimum z dokładnością większą niż 0.01 (3 cyfry znaczące). A może przyczyną jest zbyt mała liczba punktów, z jakich utworzyliśmy wykres? Zmniejszmy odstęp między nimi z 0.01 do 0.001:
```
N = 10001;
```
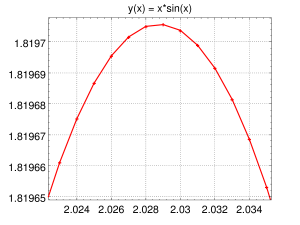
  Aby uzyskać “ładny” wykres, z dopasowaną skalą na osi “y”, zamiast klikać na wykres, wybierałem myszką prostokąt, który miał być powiększony. Teraz możemy oszacować, że pierwsze maksimum występuje dla $x\approx 2.029$ . Problem jednak w tym, że zmianie $\Delta x = 0.001$ odpowiada $\Delta y \approx 0.00001$ (a nawet jeszcze mniejsza w bezpośrednim otoczeniu maximum), czyli przyrost y jest znacznie mniejszy, rzędu $(\Delta x)^2$ . Oznacza to, że na maszynie, która przechowuje liczby z dokładnością do 16 cyfr znaczących, nie mamy żadnych szans wyznaczyć położenie maksimum z dokładnością większą niż około 7-8 cyfr znaczących – niezależnie od gęstości siatki punktów kontrolnych.
  OK, wykonaj podobny wykres dla drugiego maksimum lub pierwszego minimum i sprawdź, że zachodzi w nim podobne zjawisko.
8. Skoro bezpośrednie wyznaczanie położenia ekstremum jest uciążliwe i podatne na błędy, próbujemy obejść tę trudność poprzez przeformułowanie problemu: zamiast szukać maksimum lub minimum bezpośrednio, będziemy szukać miejsc zerowych pochodnej funkcji y(t).
  Zdefiniuj funkcję v(t) jako pochodną y(t):
```
v = @(x) (...);
```
  oczywiście w powyższym kodzie trzy kropki należy zastąpić jakąś użyteczną treścią.
9. Wykonaj rysunek $y(t)$ i $v(t)$ .
10. Wyznacz wszystkie punkty zerowe funkcji $v(t)$ (znaną już funkcją fzero). Zapisz gdzieś ich wartości, bo przydadzą się później, w kolejnym zdaniu.
11. Na pewno ciekawi Cię, z jaką dokładnością Octave wyznaczyło miejsca zerowe v(t)? Odpowiedź można uzyskać, wywołując fzero w specjalny sposób:
```
>> [X, FVAL, INFO, OUTPUT] = fzero(v, 2)
X =  2.02875783811044
FVAL =  -4.44089209850063e-015
INFO =  1
OUTPUT =
  scalar structure containing the fields:
    iterations =  7
    funcCount =  10
    bracketx =
       2.02875783811043   2.02875783811044
    brackety =
      3.33066907387547e-016  -4.44089209850063e-015
```
  Składowa OUTPUT.bracketx informuje, że miejsce zerowe funkcji $v(t)$ znajduje się pomiędzy 2.02875783811043 a 2.02875783811044, jego wartość została więc wyznaczona z dokładnością do 15 cyfr znaczących. W analogiczny sposób zbadaj dokładność wyznaczenia innego miejsca zerowego $v(t)$ .
12. Kolej na punkty przegięcia. Zdefiniuj $a(t)$ jako pochodną $v(t)$ .
13. Wykonaj rysunek $x(t), v(t)$ oraz $a(t)$
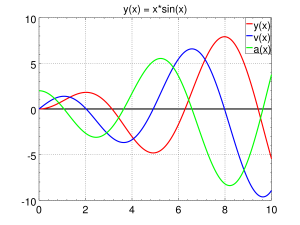
14. Znaną metodą wyznacz miejsca zerowe $a(t)$ . Czy odpowiadają one punktom, w których $v(t)$ ma minimum lub maksimum?
15. Ile wynosi globalne minimum i maksimum $x(t)$ na badanym przedziale $0 \le t \le 10$ ?
16. Położenie pewnego obiektu, który porusza się po linii prostej wzdłuż osi x, dane jest równaniem
  $x(t) = t\sin(t),$
  gdzie położenie (x) mierzone jest w metrach, a czas (t) – w sekundach. Jaką drogę, z dokładnością do 0.01 metra, przebył ten obiekt w ciągu pierwszych 10 sekund ruchu?
  Wskazówka: w poprawnej odpowiedzi cyfra 4 występuje 2 razy.